機械学習エンジニアがよく使う表現として「ゴミを入れればゴミしか出てこない」という言葉があります。これは機械学習の特性を表しており、ここで言うゴミとは予測の役に立たないデータを表しています。
一般的なWEBアプリーケーションの開発であれば、機能実装の方法は概ね決まっています。例えばログイン機能を実装するのに細かい仕様の違いはあるにせよ、実装手段に大きな違いはありません。ですが、機械学習ではそのようにはいきません。
機械学習の中心となる存在は「データ」であり、扱うデータが違えば手法も大きく異なります。加えてデータそのものに対しても「工夫」が必要となります。
このデータに対して行う工夫こそ、今回の記事の主題である「特徴選択」です。世界中のデータサイエンティストが予測精度を競い合うKaggleなどでも、上位にランクインする方々はこの特徴選択(または特徴エンジニアリング)のテクニックを駆使しています。
本記事では機械学習の初心者を対象に特徴選択の概要や手法をまとめました。機械学習を勉強していると「どうすれば予測精度を改善することができるのか?」と頭を悩ましたことはありませんか?その答えは特徴選択にあるかもしれません。
この記事の目次 [隠す]
そもそも特徴量とは何か?
特徴選択ですが英語では「Feature Selection(フューチャー・セレクション)」と呼ばれています。また日本語でも「特徴量選択」や「変数選択」、さらに「特徴削減」「属性選択」などと複数の呼び名があります。
では、そもそもこの特徴量とは何かをまずは簡単に説明をします。特徴量をご存知の方は次のセクションへ読み飛ばしてください。
機械学習における特徴量とは、学習の入力に使う測定可能な特性のことです。より明確に理解をするため2つの簡単な例題を使って説明をします。
物件条件から家賃を予測する
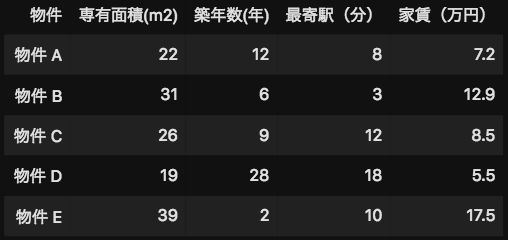
下のデータをご覧ください。これは、とある地域の賃貸物件の条件と家賃です。賃貸物件は様々な条件で家賃が決まっています。例えば、物件の専有面積が増えるほど家賃は高くなる傾向にあり、逆に築年数は増えるほど家賃は安くなる傾向にあります。
このように予測したい家賃の「特徴」となるデータを機械学習では「特徴量」と呼びます。下記のデータでは「専有面積」「築年数」「最寄駅」の3つのデータが特徴量です。
天気予報から売上を予測する
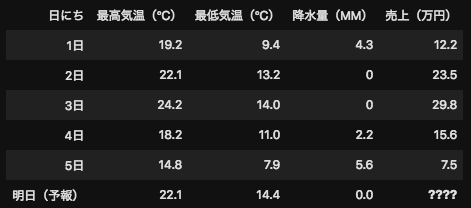
もう一つ簡単な事例として下記のデータをみましょう。こちらは、アイスクリーム屋さんの日別の売上と天気データです。この事例では機械学習の手法を利用して天気データから売上を予測することが目的です。
つまり、ここでの特徴量とは売上に対して関係性がある(もしくはあると予想される)「最高気温」「最低気温」「降水量」の3つのデータを特徴量と呼びます。
特徴量がお判り頂けたかと思います。特徴量とは機械学習の予測精度に非常に重要な役割を持っています。
特徴選択とは?
特徴選択とは機械学習モデルの予測精度の改善を目的として、訓練データの中からターゲットの予測により強い関連がある特徴を選択することをいいます。
上記の家賃予測や売上予測では特徴量は2〜3個でした。実社会の機械学習のプロセスでは、この特徴量が数千、場合によっては数万から数百万あるケースがあります。
例えば工場での異常検知を考えてみましょう。とある工程では5個のセンサーを使って製品管理をしており、この5つのセンサーの全ての値を特徴量として機械学習モデルを構築して異常検知を行いました。

5個センサー(特徴量)で異常検知を行ったところ、正しく異常を検知できた正解率は70%でした。より精度の高い異常検知を行いたいと考えた工場長は、センサーを1万個に増やしました。
では、ここで考えてみて下さい。この1万個のセンサーの全ての値が異常検知に平等に役立ちますか?可能性としては低いですよね。異常が発生しやすい近辺のセンサーや、異常の原因となる作業付近のセンサーの値の方が異常検知をするのに役に立ちそうです。
そこで、センサー(特徴量)が異常検知(ターゲット)に対してどれくらい役立つかを調べて、機械学習モデルへ学習させるセンサーを選別する作業を「特徴選択」と呼びます。
特徴選択で特徴量を減らすことによって、予測に必要のない特徴を取り除いて、重要な特徴だけを残すことができます。同じく特徴量を減らす方法に特徴量エンジニアリングという手法もありますが、こちらはまた別の機会に取り上げたいと思います。
特徴選択はなぜ必要なの?目的とは?
データが大きかったり特徴量が多いとなおさらデータの品質は重要になってきます。高精度な学習モデルを作るのに、手元にあるデータ全部を機械に学習させる必要はありません。
データ内のノイズは学習モデルの精度向上に関係ないばかりか、場合によっては精度を下げてしまうこともあります。ノイズを除去することによって、機械は予測対象に関連のある特徴のみを学習できるので、予測の精度も上がるというわけです。
特徴選択の最大の目的はモデルの予測精度の向上ですが、それ以外にも下記の目的もあります。
- 学習データを縮小することによって学習にかかる時間を短縮できる
- モデルの構造を単純化し理解しやすくできる
- 過学習を防ぐことができる
では、具体的にどのように特徴量が有益か無益かを判断するのでしょうか?先ほどの1万個センサーで異常検知を行う例で考えると、一つ一つのセンサーのデータを確認するのは現実的ではありません。
次のセクションでは特徴選択の一般的な3種類の手法を説明します。なお、本記事では数式の説明は割愛して、手法の概念と仕組みに焦点を当てて説明させていただきます。
フィルタ法(Filter Method)とは?
フィルタ法では、統計のテクニックを用いて各特徴の「予測に使える度合」を点数化します。点数をもとに特徴にランク付けを行い、予測に使うか否かをそれぞれ決定していきます。
なお、点数を決めるのにもいくつか方法があり、特徴と予測対象の関係性を見て決める方法もあれば、特徴だけを見て統計的に決める方法もあります。欠点としては、特徴を1つずつしか見られないので、複数の特徴量の併用効果は考慮されないことが挙げられます。(例:センサーAとセンサーBを併用して異常検知を行うと精度が向上するがフィルタ法では考慮されない)
各特徴量の点数を決める方法ですが、特徴量とターゲットのデータ型により手法が異なります。主な手法としては「カイ二乗検定(Chi-Square)」や「ANOVA(Analytics of Variance)」などがあります。
参考までにですが、機械学習クラウドサービスのマイクロソフトAzure Machine Learning Studioではフィルタ法として7つの手法が用意されています。このように知識と経験が必要な特徴選択のプロセスを単純化して実装できるのは、クラウドサービスの良いメリットですね。
ラッパー法(Wrapper Method)とは?
ラッパー法では複数の特徴を同時に使って予測精度の検証を行い、精度が最も高くなるような特徴量の組み合わせを探索していきます。様々な組み合わせでそれぞれ学習を行わせ、その学習結果をもとに組み合わせに優劣をつけていきます。
イメージとしては「下手な鉄砲も数打ちゃ当たる」作戦と似ており、様々な特徴量を使って予測を繰り返して、精度が高くなる特徴量へ絞っていく手法です。
上記の仕組みを理解すると想像しやすいですが、ラッパー法では計算の負荷が大きくなる傾向にあります。つまり、特徴量が多い場合は計算に非常に時間を要するという弱点も理解しておきましょう。異常検知の事例ではセンサーが1万個でしたが、これが100万個あるとすれば、ラッパー法で特徴量を選択するには非常に膨大な計算が必要となります。
ラッパー法にも計算方法は複数の手法があります。下記は基本的な2つの手法となります。
前進法(Forward Search)
前進法では、まず全ての特徴量を学習データから取り除いた状態からスタートします。そこから、精度の向上が一番大きくなるような、最も有用な特徴を1つずつ足していきます。これを、精度の変化がなくなるまで反復的に繰り返します。
後退法(Backward Elimination)
後退法では、まず全ての特徴を学習データに含めた状態からスタートします。そこから、精度の向上が一番大きくなるような、最も不要な特徴を1つずつ取り除いていきます。これを、精度の変化がなくなるまで反復的に繰り返します。
組み込み法(Embedded Method)とは?
組み込み法はフィルタ法とラッパー法の2つの強みを掛け合わせたような手法で、機械学習モデルが学習の一環として特徴の選択を行います。
上2つの方法と違い、そもそもの学習アルゴリズムに特徴量選択が組み込まれているので、学習と特徴量選択を同時に行うことができます。使われるアルゴリズムですが「ラッソ回帰(LASSO Linear Regression)」や「決定木」などがあります。各アルゴリズムの詳細は割愛しますが、詳しく学びたい方は下記のリンクをご参照ください。
実践チュートリアル5つのデータセットを使って決定木とランダムフォレストを徹底解説
まとめ
今回の記事では特徴量選択について機械学習初心者向けに概要の解説を行いました。機械学習はデータが命と言っても過言ではありません。どんなに高性能な学習モデルでも、正しい特徴量選択のされていないデータでは思うような結果は出ません。
冒頭でも触れましたが上級のデータサイエンティスト/機械学習エンジニアは、全員と言って良いほど「特徴選択」を巧みに駆使しています。
下記のチュートリアルでは「ランダムフォレスト」を使って、実際のデータから特徴選択を行う流れも説明していますので、是非ご参考ください!