コインチェック社の大量の仮想通貨盗難事件を筆頭に、日本でも大きく報道されている仮想通貨。ことビットコインに絞れば、日本は世界No1の取引高となっており、まだまだ仮想通貨バブルは続きそうな予感です。
今回の記事では、「機械学習で仮想通貨（ビットコインとイーサリアム）の価格を予測してみよう」という趣旨となります！ 原則として機械学習を触ったことがないエンジニアの方でも実行できるように説明をしていますので、初めて機械学習を触る方でも、是非挑戦してみてください！
本記事では「入門編」としまして、機械学習で仮想通貨の予測をこれから取り組もうと考えている方への最初の一歩となれば幸いです。仮想通貨のデータセットの入手方法や、予測モデルの考え方、またKerasを使って実際にLSTMを構築してテストデータを評価してみます。（本記事はロンドン在住の凄腕データーサイエンティストであるDavid Sheehanさんの記事をご本人の承諾のもと参考にしてます。）
＊免責事項＊
本記事は機械学習の習得を目的としたチュートリアルとなります。仮想通貨への取引への勧誘を目的に作成したものではありません。また本情報を参考・利用して行った投資等の一切の取引につきましては、利用者ご自身の責任において行われるようお願いいたします。
では、まずは本チュートリアルの概要から説明していきます。
機械学習で予測する仮想通貨の種類と汎用性
現在、世界中に出回っている仮想通貨の種類は600種類を超えています。今回コインチェック社から盗難されたNEM（ネム）も仮想通貨の一つです。本記事では全世界で取引額が圧倒的に多い上位2位の仮想通貨、「ビットコイン」と「イーサリアム」の価格予想を機械学習を使って行います。
上記2つの仮想通貨以外にも、機械学習で予測してみたいという方も多いかと思います。ですので、今回は静的なデータを使用せず、仮想通貨の価格を提供しているcoinmarketcap.comから価格データを取得する方を採用しています。コードを少し変更するだけで、他の通貨への拡張も可能です。
予測モデルに使用する手法について
本チュートリアルでは、ディープラーニングの手法の一つ「LSTM（エル・エス・ティー・エム）」を「Keras（ケラス）」を使用して構築します。LSTMとは、Long Short Term Memoryの略で、ディープラーニングにおいて、メジャーな手法の一つです。
LSTMですが、ざっくりと説明をすると「短期記憶を長期に渡って活用することが可能」な手法で、特に時系列データを扱うのに優れています。つまり、今回予測を行う仮想通貨の価格予想のような時系列のデータに適しています。（時系列データに適してるモデルはLSTM以外にもありますが。）
またLSTMのモデル構築にKerasを使用します。Kerasとは、TensorFlowをバックエンドとして非常に簡単に、かつ高水準のニューラルネットワークの構築が可能なオープンソスライブラリとなります。機械学習関係のライブラリには珍しく、日本語でのドキュメントが提供されているのは嬉しいですね。
実行環境の詳細と所要時間
下記の環境で実行しています。コードを書くことを含めて10時間〜20時間程度を要します。記事中でも特に重い処理に関しては注釈を入れています。Amazon SageMakerなどのクラウド環境が整っている方は、そちらの環境をお使い頂いた方が良いかと思います。（CPUマシーンでも実行は可能ですが。）
- macOS High Sierra 10.13.1
- プロセッサ 2.4GHz Intel Core i5
- メモリ 8GB
- Python 3.6.1
- Numpy 1.12.1
- Pandas 0.20.1
- Matplotlib 2.0.2
- iPython 6.2.1
- seaborn 0.8.1
- Pillow 1.1.7
- h5py 2.7.1
では、早速データセットを作成して機械学習で仮想通貨の価格予想をしてみましょう！
ビットコインとイーサリアムのデータセット作成
仮想通貨ですが、さすが全世界で話題となっているだけあり、データを揃えるのはさほど難しくありません。例えば、ビットコインでしたらKaggleで2〜3年の1分単位の価格とその他の指標データが公開されています。（参考：Kaggle 初心者が知っておくべき3つの使い方）
さて本チュートリアルで使うデータですが、前述した通り、CSVなどの静的データを利用せずに、ウェブサイトやAPIをからデータを取得する方法を採用します。静的データだと、他の通貨へ適用をする場合や期間の調整を行う際に一手間かかり面倒です。APIなどを利用すれば、拡張・調整が簡単に行えます。
ということで、ウェブサイトを利用するのですが、今回はcoinmarketcap.comを活用しましょう。こちらのサイトですが、なんと1511種類の仮想通貨ペアの情報を配信しています。また、各通貨ごとに取引額が多い仮想通貨販売所（または交換所）もリストしています。機械学習には関係ないですが、これはこれで面白いですね（笑）
CoinMarketCap（コインマーケットキャップ）では、APIの配信もしていますが、今回はサイトから情報をスクレイピングしてデータセットを作成します。サイト上のデータの利用や取り扱いに関しては、免責事項(英語)とFAＱ(英語)をご確認ください。コインマーケットキャップのデータですが、商用利用でも無料で利用が可能です。
では、早速、必要なライブラリをインポートして仮想通貨のデータセットを作成してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import pandas as pd import time import seaborn as sns import matplotlib.pyplot as plt import datetime import numpy as np # コインマーケットキャップからデータをスクレイピング bitcoin_market_info = pd.read_html("https://coinmarketcap.com/currencies/bitcoin/historical-data/?start=20130428&end="+time.strftime("%Y%m%d"))[0] # Dateを文字列から日付フォーマットへ変換 bitcoin_market_info = bitcoin_market_info.assign(Date=pd.to_datetime(bitcoin_market_info['Date'])) # 取引高が'-'の欠損データを0へ変換 bitcoin_market_info.loc[bitcoin_market_info['Volume']=="-",'Volume']=0 # イントへ変換 bitcoin_market_info['Volume'] = bitcoin_market_info['Volume'].astype('int64') # データセットのヘッド情報の確認 bitcoin_market_info.head() |
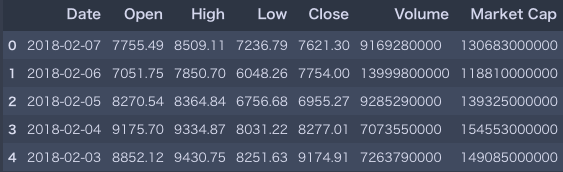
ビットコインのデータセットをサイトから取得できましたので、次は同じ要領でイーサリアムのデータセットもスクレイピングしましょう。
|
|
# イーサリアムの価格データを所定のURLからスクレイピング eth_market_info = pd.read_html("https://coinmarketcap.com/currencies/ethereum/historical-data/?start=20130428&end="+time.strftime("%Y%m%d"))[0] # データの処理とヘッド情報の表示 eth_market_info = eth_market_info.assign(Date=pd.to_datetime(eth_market_info['Date'])) eth_market_info.head() |
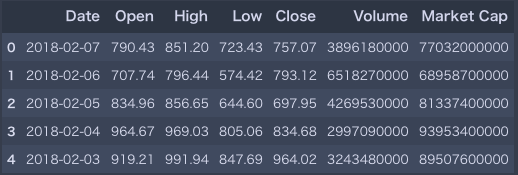
これでデータの取得は完了です。最初に必要なライブラリをインポートして、コインマーケットキャップのこちらの価格リストページから、Pandasのread_htmlを使用してスクレイピングしています。データがローカルに落ちたら、日付やイントなど、必要なデータ型のクレンジングを行いました。
データが揃いましたので、ビットコインとイーサリアムのロゴを取得して、両通貨のデータをプロッティングしてみましょう。Pillowですが、ロゴ取得のために利用しています。見た目が変わるだけなので、不必要な方はスキップしていただいて問題ありません。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# ビットコインとイーサリアムのロゴを取得しましょう import sys from PIL import Image import io if sys.version_info[0] < 3: import urllib2 as urllib bt_img = urllib.urlopen("http://logok.org/wp-content/uploads/2016/10/Bitcoin-Logo-640x480.png") eth_img = urllib.urlopen("https://upload.wikimedia.org/wikipedia/commons/thumb/0/05/Ethereum_logo_2014.svg/256px-Ethereum_logo_2014.svg.png") else: import urllib bt_img = urllib.request.urlopen("http://logok.org/wp-content/uploads/2016/10/Bitcoin-Logo-640x480.png") eth_img = urllib.request.urlopen("https://upload.wikimedia.org/wikipedia/commons/thumb/0/05/Ethereum_logo_2014.svg/256px-Ethereum_logo_2014.svg.png") image_file = io.BytesIO(bt_img.read()) bitcoin_im = Image.open(image_file) image_file = io.BytesIO(eth_img.read()) eth_im = Image.open(image_file) width_eth_im , height_eth_im = eth_im.size eth_im = eth_im.resize((int(eth_im.size[0]*0.8), int(eth_im.size[1]*0.8)), Image.ANTIALIAS) |
|
|
# ビットコインとイーサリアムのデータフレームのカラム名を変更 bitcoin_market_info.columns =[bitcoin_market_info.columns[0]]+['bt_'+i for i in bitcoin_market_info.columns[1:]] eth_market_info.columns =[eth_market_info.columns[0]]+['eth_'+i for i in eth_market_info.columns[1:]] |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#ビットコインの価格をプロッティング fig, (ax1, ax2) = plt.subplots(2,1, gridspec_kw = {'height_ratios':[3, 1]}) ax1.set_ylabel('Closing Price ($)',fontsize=12) ax2.set_ylabel('Volume ($ bn)',fontsize=12) ax2.set_yticks([int('%d000000000'%i) for i in range(10)]) ax2.set_yticklabels(range(10)) ax1.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,7]]) ax1.set_xticklabels('') ax2.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,7]]) ax2.set_xticklabels([datetime.date(i,j,1).strftime('%b %Y') for i in range(2013,2019) for j in [1,7]]) ax1.plot(bitcoin_market_info['Date'].astype(datetime.datetime),bitcoin_market_info['bt_Open']) ax2.bar(bitcoin_market_info['Date'].astype(datetime.datetime).values, bitcoin_market_info['bt_Volume'].values) fig.tight_layout() fig.figimage(bitcoin_im, 100, 120, zorder=3,alpha=.5) plt.show() |
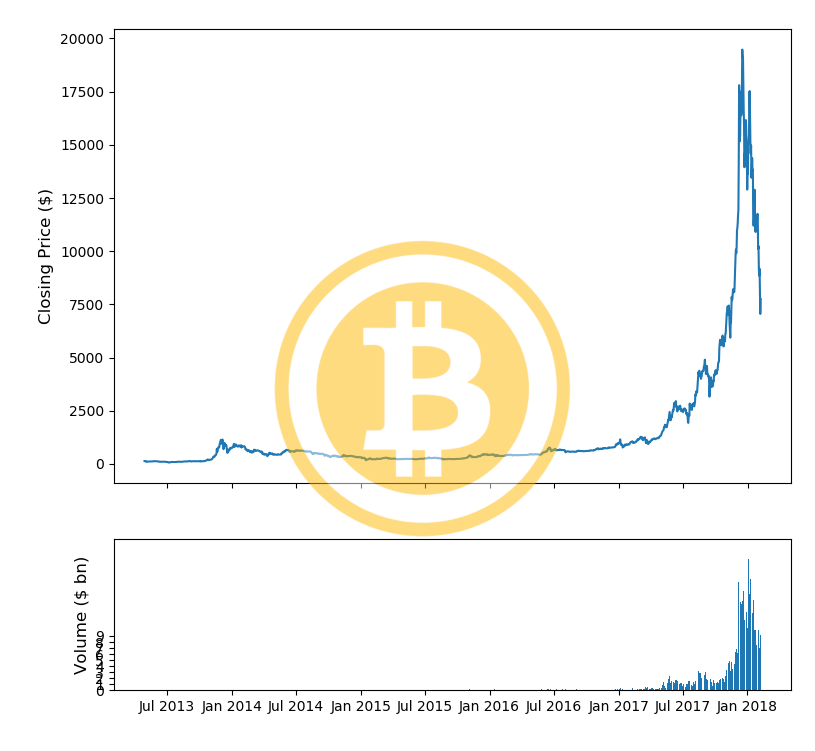
ロゴも表示されて綺麗にプロッティングされていますね。同様のプロットをイーサリアムでも作成してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
fig, (ax1, ax2) = plt.subplots(2,1, gridspec_kw = {'height_ratios':[3, 1]}) #ax1.set_yscale('log') ax1.set_ylabel('Closing Price ($)',fontsize=12) ax2.set_ylabel('Volume ($ bn)',fontsize=12) ax2.set_yticks([int('%d000000000'%i) for i in range(10)]) ax2.set_yticklabels(range(10)) ax1.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,7]]) ax1.set_xticklabels('') ax2.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,7]]) ax2.set_xticklabels([datetime.date(i,j,1).strftime('%b %Y') for i in range(2013,2019) for j in [1,7]]) ax1.plot(eth_market_info['Date'].astype(datetime.datetime),eth_market_info['eth_Open']) ax2.bar(eth_market_info['Date'].astype(datetime.datetime).values, eth_market_info['eth_Volume'].values) fig.tight_layout() fig.figimage(eth_im, 300, 180, zorder=3, alpha=.6) plt.show() |
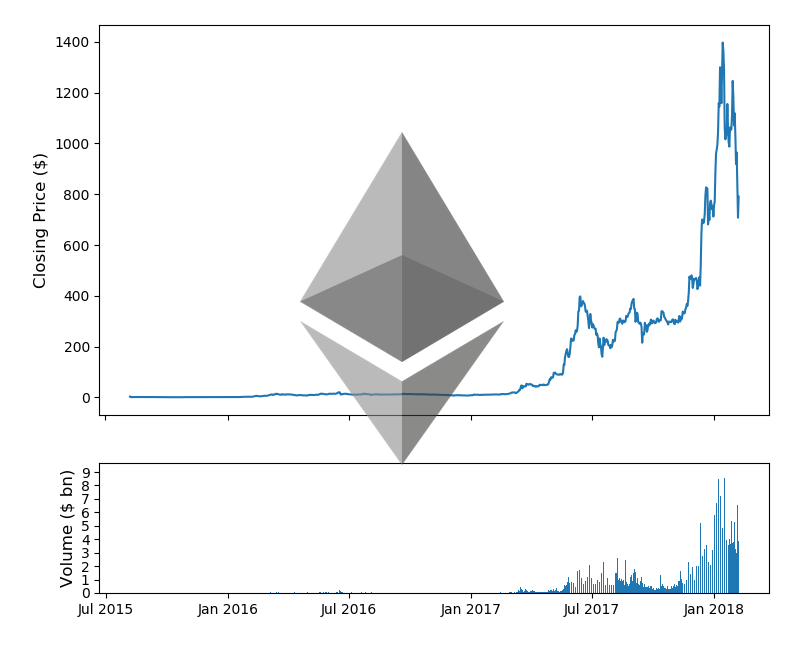
イーサリアムの価格も表示されました。両通貨共に過去の価格から現在の価格まで1日単位でデータを取得しています。価格だけでなく、取引量（Volume）も取得しています。このようにプロットにしてみると、価格が急激に高騰しているのがよくわかりますね。また取引量も2017年に入ってから激増しています。
最後に、両方の通貨の価格データを結合処理して一つのデータフレームで扱えるようにしましょう。また、day_diffとして同日のオープンとクローズの差をオープンで割った指標も追加しておきましょう。
|
|
market_info = pd.merge(bitcoin_market_info,eth_market_info, on=['Date']) market_info = market_info[market_info['Date']>='2016-01-01'] for coins in ['bt_', 'eth_']: kwargs = { coins+'day_diff': lambda x: (x[coins+'Close']-x[coins+'Open'])/x[coins+'Open']} market_info = market_info.assign(**kwargs) market_info.head() |
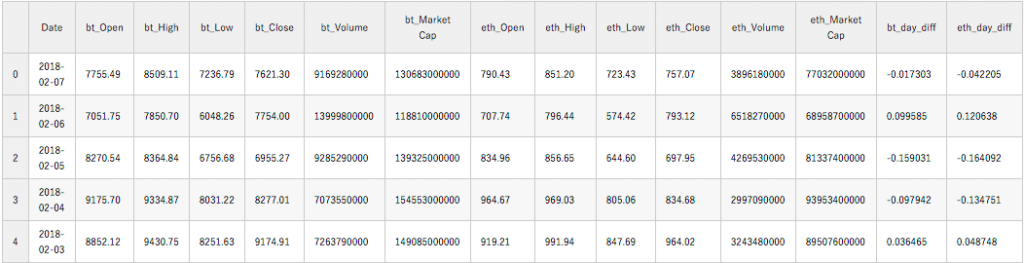
これで、データセットの作成は完了です。次のステップへ進みましょう。
機械学習じゃない予測手法を考えてみよう
次は仮想通貨の価格の基本的な予測手法について考えてみましょう。その前に、まずはデータセットの訓練用と評価用に分けてあげる作業を行いましょう。
機械学習では、一般的にデータを「トレーニング（訓練用）」と「テスト（評価用）」の2つに分けます。「トレーニング」のデータにフィットしたモデルで、今度は全く新しい「テスト」のデータを使って予測を行うことで、そのモデルの評価を行うためです。
仮想通貨の価格のような「時系列データ」を扱うタイムシリーズモデルでは、一般的に「トレーニング」と「テスト」を時間で区切ってデータを分けます。今回は2017年10月1日を境にデータを分けてみましょう。（この日付が正しいという訳ではなく、適当に考えたスプリットポイントです）
データスプリットの処理はLSTMのモデル構築前にやるとして、スプリットをする場合、各データがどのような分布になるかプロッティングして確認してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
split_date = '2017-10-01' fig, (ax1, ax2) = plt.subplots(2,1) ax1.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,7]]) ax1.set_xticklabels('') ax2.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,7]]) ax2.set_xticklabels([datetime.date(i,j,1).strftime('%b %Y') for i in range(2013,2019) for j in [1,7]]) ax1.plot(market_info[market_info['Date'] < split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date'] < split_date]['bt_Close'], color='#B08FC7', label='Training') ax1.plot(market_info[market_info['Date'] >= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date'] >= split_date]['bt_Close'], color='#8FBAC8', label='Test') ax2.plot(market_info[market_info['Date'] < split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date'] < split_date]['eth_Close'], color='#B08FC7') ax2.plot(market_info[market_info['Date'] >= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date'] >= split_date]['eth_Close'], color='#8FBAC8') ax1.set_xticklabels('') ax1.set_ylabel('Bitcoin Price ($)',fontsize=12) ax2.set_ylabel('Ethereum Price ($)',fontsize=12) plt.tight_layout() ax1.legend(bbox_to_anchor=(0.03, 1), loc=2, borderaxespad=0., prop={'size': 14}) fig.figimage(bitcoin_im.resize((int(bitcoin_im.size[0]*0.65), int(bitcoin_im.size[1]*0.65)), Image.ANTIALIAS), 200, 260, zorder=3,alpha=.5) fig.figimage(eth_im.resize((int(eth_im.size[0]*0.65), int(eth_im.size[1]*0.65)), Image.ANTIALIAS), 350, 40, zorder=3,alpha=.5) plt.show() |
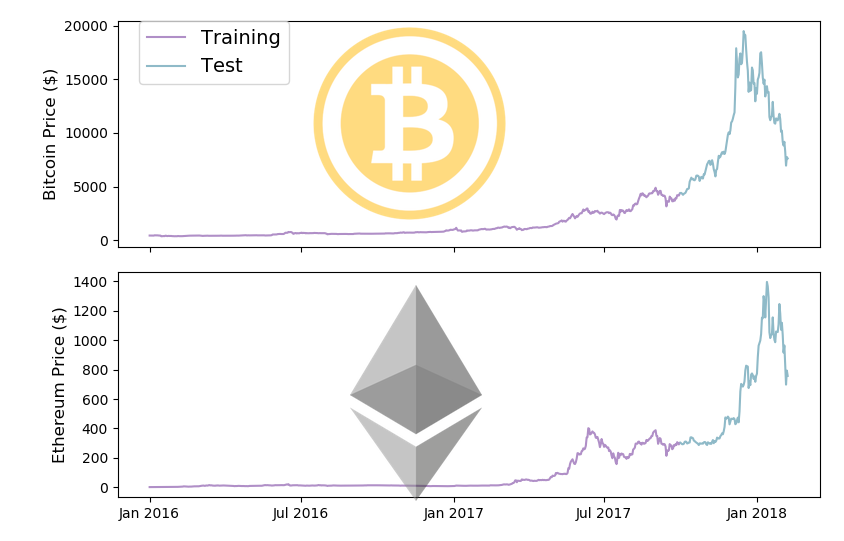
このようにしてみると、トレーニングデータのほとんどの期間で、大きな価格変動がありませんね。ここは今後に改善余地がありそうですが、今回はこのまま進めましょう。
さて、では本題に戻りましょう。ディープラーニングで仮想通貨の価格を予測する前に、まずはもっと単純な予測手法を考えてみましょう。下のグラフは、最も単純な手法を用いて価格を予測したものをプロッティングしたものです。（Acutualは実際の価格で、Predictedが予測価格です）
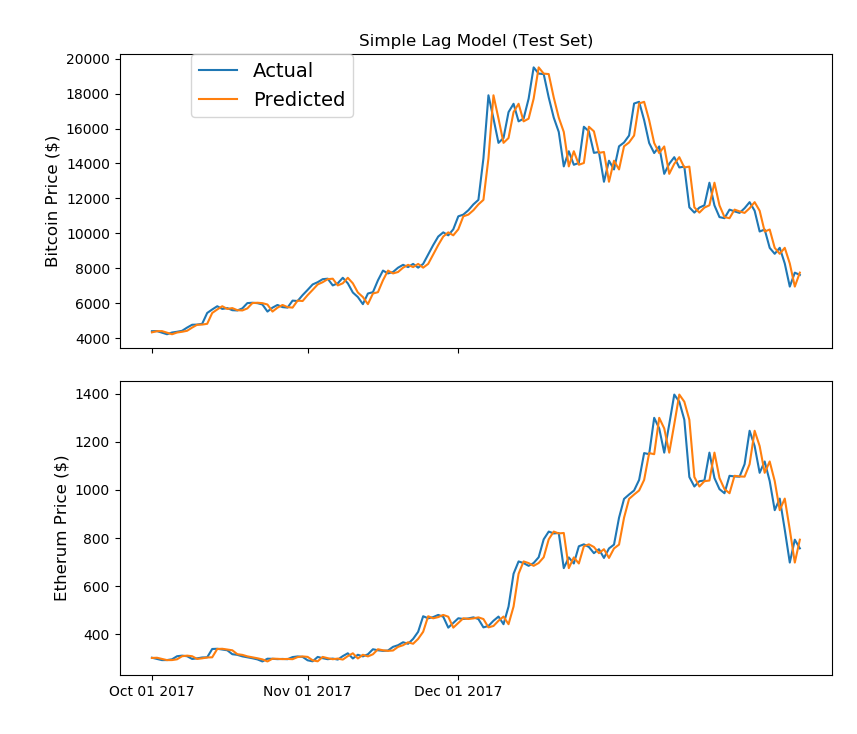
どうでしょうか？Acutual（実際のプライス）のラインと予測ラインが非常に類似しており、かなり上手く予測されていると思いませんか？こんな正確な予測が出来れば、億り人なんて楽勝だ！と思いませんか？（笑）
実はこの予測ですが・・前日の価格をそのまま翌日の予想価格としただけです。「遅れる」を意味する「Lag」をとって、「Lag Model（ラグ・モデル）」と呼ばれています。
こちらが、ラグモデルのコードです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 前日の価格を翌日の予想価格として扱うラグモデルの予測プロッティング fig, (ax1, ax2) = plt.subplots(2,1) ax1.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax1.set_xticklabels('') ax2.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax2.set_xticklabels([datetime.date(2017,i+1,1).strftime('%b %d %Y') for i in range(12)]) ax1.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= split_date]['bt_Close'].values, label='Actual') ax1.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= datetime.datetime.strptime(split_date, '%Y-%m-%d') - datetime.timedelta(days=1)]['bt_Close'][1:].values, label='Predicted') ax1.set_ylabel('Bitcoin Price ($)',fontsize=12) ax1.legend(bbox_to_anchor=(0.1, 1), loc=2, borderaxespad=0., prop={'size': 14}) ax1.set_title('Simple Lag Model (Test Set)') ax2.set_ylabel('Etherum Price ($)',fontsize=12) ax2.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= split_date]['eth_Close'].values, label='Actual') ax2.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= datetime.datetime.strptime(split_date, '%Y-%m-%d') - datetime.timedelta(days=1)]['eth_Close'][1:].values, label='Predicted') fig.tight_layout() plt.show() |
単純に前日のデータを予測値として使うだけで、これだけフィットしている予測モデルに見えるのは驚きですよね。次は、この前日の価格をそのまま翌日の価格として予測するラグモデルを少し拡張してみましょう。
株などの価格は一般的に「ランダム・ウォーク」として扱われます。「ランダム・ウォーク」とは、次に現れる位置が確率的にランダムに決定される運動をさします。このランダム・ウォークを平均値と標準偏差を使って定義したモデル「ランダム・ウォーク・モデル」を次は試してみましょう。（ランダム・ウォークの定義をより詳しく知りたい方は、詳しくはこちらのPDF(英語)ご参照ください）（平均値や標準偏差などの統計用語に不安がある方は、統計入門コース前編をご参照ください）
まずは、ビットコインとイサーリアムの日毎の価格変動が正規分布になっているかどうかを、ヒストグラムにプロッティングして確認をしましょう。（正規分布は統計入門後編で詳しく扱ってます）
|
|
fig, (ax1, ax2) = plt.subplots(1,2) ax1.hist(market_info[market_info['Date']< split_date]['bt_day_diff'].values, bins=100) ax2.hist(market_info[market_info['Date']< split_date]['eth_day_diff'].values, bins=100) ax1.set_title('Bitcoin Daily Price Changes') ax2.set_title('Ethereum Daily Price Changes') plt.show() |
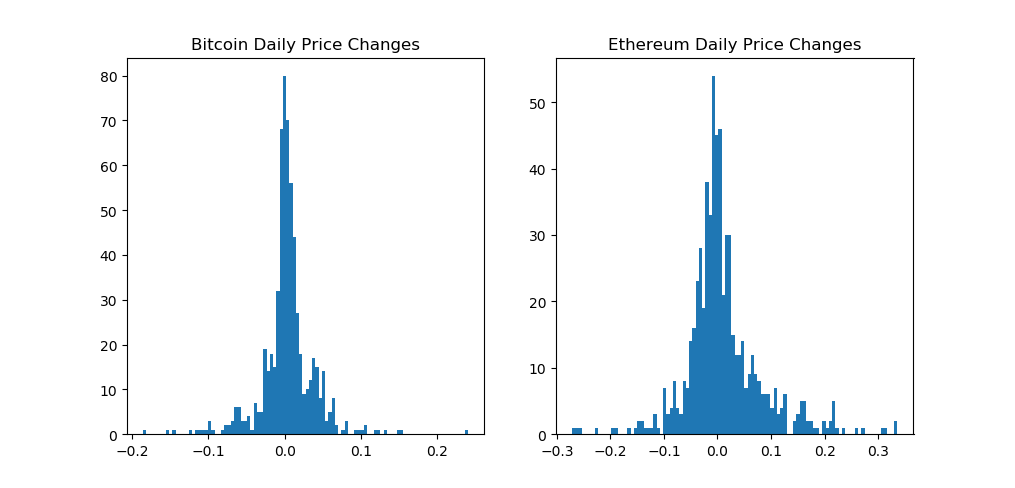
次に、ランダム・ウォーク・モデルでビットコインとイーサリアムの価格を予測してみましょう。ランダムウォークの処理ですが、トレーニング期間（2017年10月以前）のデータと平均値と標準偏差を処理して、そのモデルをテスト期間（2017年10月以降）に適用して予想価格としてプロッティングしています。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
np.random.seed(202) bt_r_walk_mean, bt_r_walk_sd = np.mean(market_info[market_info['Date']< split_date]['bt_day_diff'].values), \ np.std(market_info[market_info['Date']< split_date]['bt_day_diff'].values) bt_random_steps = np.random.normal(bt_r_walk_mean, bt_r_walk_sd, (max(market_info['Date']).to_pydatetime() - datetime.datetime.strptime(split_date, '%Y-%m-%d')).days + 1) eth_r_walk_mean, eth_r_walk_sd = np.mean(market_info[market_info['Date']< split_date]['eth_day_diff'].values), \ np.std(market_info[market_info['Date']< split_date]['eth_day_diff'].values) eth_random_steps = np.random.normal(eth_r_walk_mean, eth_r_walk_sd, (max(market_info['Date']).to_pydatetime() - datetime.datetime.strptime(split_date, '%Y-%m-%d')).days + 1) fig, (ax1, ax2) = plt.subplots(2,1) ax1.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax1.set_xticklabels('') ax2.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax2.set_xticklabels([datetime.date(2017,i+1,1).strftime('%b %d %Y') for i in range(12)]) ax1.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= split_date]['bt_Close'].values, label='Actual') ax1.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[(market_info['Date']+ datetime.timedelta(days=1))>= split_date]['bt_Close'].values[1:] * (1+bt_random_steps), label='Predicted') ax2.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= split_date]['eth_Close'].values, label='Actual') ax2.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[(market_info['Date']+ datetime.timedelta(days=1))>= split_date]['eth_Close'].values[1:] * (1+eth_random_steps), label='Predicted') ax1.set_title('Single Point Random Walk (Test Set)') ax1.set_ylabel('Bitcoin Price ($)',fontsize=12) ax2.set_ylabel('Ethereum Price ($)',fontsize=12) ax1.legend(bbox_to_anchor=(0.1, 1), loc=2, borderaxespad=0., prop={'size': 14}) plt.tight_layout() plt.show() |
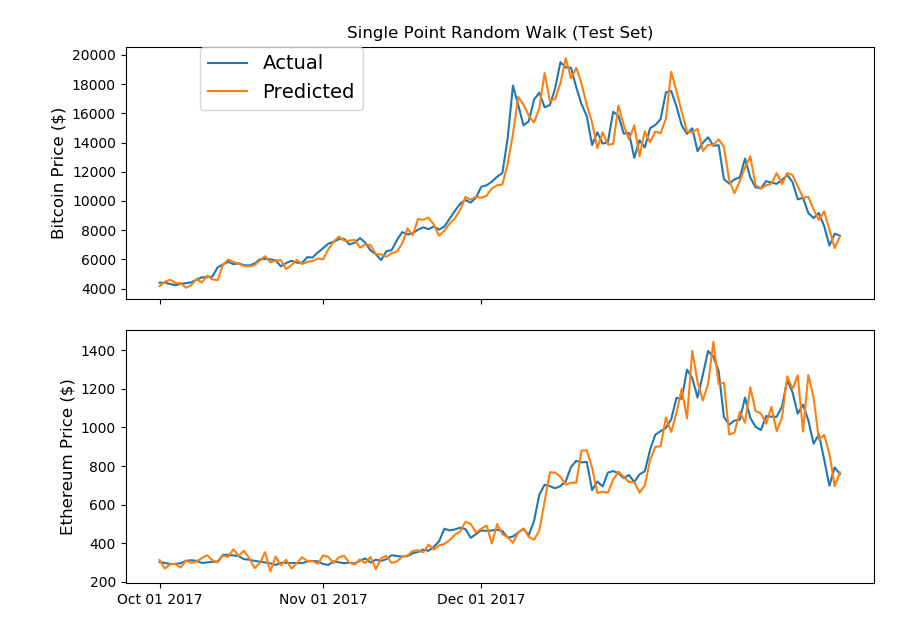
おお！なんか、それっぽい予測ラインですね（笑）なんとな〜くではありますが、両方の仮想通貨共に予測がそれなりにできていますね。さて、このランダム・ウォーク・モデルをもう少し深掘りして考えてみましょう。
上にプロッティングした予測モデルのように、翌日という一点のみを予測するモデルの評価ですが、誤解を招くほど正確に見えてしまいます。なぜなら、予測した価格と実際の価格の残差（予測と実際の差）が次の予測には適用されないからです。どれだけ残差が大きくても、次の日にはリセットされてしまうのです。特に上の例でいうと、ビットコインの価格変動幅が大きいため、予測ラインがスムースになり、優れている予測モデルに見えてしまいますよね。
タイムシリーズモデル（時系列データの予測）で、このように一点のポイント（この場合だと翌日の価格のみ）を予測することは頻繁にありますが、上記のように一点（翌日のみ）の予測モデルを評価すると、騙されたように高い評価になってしまいます。より正しくモデルの評価をするため、複数のポイント（この場合だと複数の日にち）の予測を評価するという手法があります。
複数の日にちを予測することで、残差（予測価格と実価格の差）は引き継がれるため、精度の低いモデルはよりペナルティを与えられることになります。では、上記のランダム・ウォーク・モデルに改善を加えて、次は全てのテスト期間を加味したモデルを作成してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
bt_random_walk = [] eth_random_walk = [] for n_step, (bt_step, eth_step) in enumerate(zip(bt_random_steps, eth_random_steps)): if n_step==0: bt_random_walk.append(market_info[market_info['Date']< split_date]['bt_Close'].values[0] * (bt_step+1)) eth_random_walk.append(market_info[market_info['Date']< split_date]['eth_Close'].values[0] * (eth_step+1)) else: bt_random_walk.append(bt_random_walk[n_step-1] * (bt_step+1)) eth_random_walk.append(eth_random_walk[n_step-1] * (eth_step+1)) fig, (ax1, ax2) = plt.subplots(2, 1) ax1.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax1.set_xticklabels('') ax2.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax2.set_xticklabels([datetime.date(2017,i+1,1).strftime('%b %d %Y') for i in range(12)]) ax1.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= split_date]['bt_Close'].values, label='Actual') ax1.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), bt_random_walk[::-1], label='Predicted') ax2.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), market_info[market_info['Date']>= split_date]['eth_Close'].values, label='Actual') ax2.plot(market_info[market_info['Date']>= split_date]['Date'].astype(datetime.datetime), eth_random_walk[::-1], label='Predicted') ax1.set_title('Full Interval Random Walk') ax1.set_ylabel('Bitcoin Price ($)',fontsize=12) ax2.set_ylabel('Ethereum Price ($)',fontsize=12) ax1.legend(bbox_to_anchor=(0.1, 1), loc=2, borderaxespad=0., prop={'size': 14}) plt.tight_layout() plt.show() |
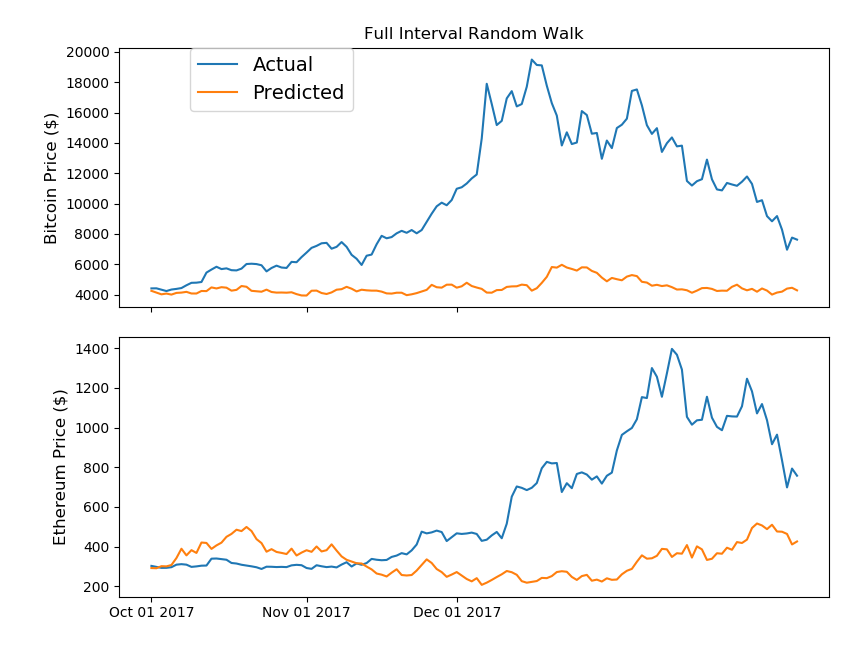期間を伸ばしたことで、シングルポイントのランダム・ウォーク・モデルよりも実価格と予測価格に大きな差が出ていますね。参考までにですが、ランダムウォークモデルは、ランダムシードの設定で大きく予測も変動します。上記のコードでは、ランダムシードをイーサリアムに照準を合わせて設定しています。余裕がある方は、ランダムシードを変えてみて、予測がどのように変動するか確認してみてください。
さて、このセクションでは機械学習を使わず、ビットコインとイーサリアムの価格予測をしてみました。次はいよいよ本題のLSTM（ディープラーニングのモデル）を使った仮想通貨の価格予測をやってみましょう！
LSTMで仮想通貨の価格予測をしてみる
ビットコインとイーサリアムの価格データにも慣れてきたところで、本題のディープラーニングを使って予測をしてみましょう。冒頭でも触れましたが、Kerasを使って構築しますので、まだ環境構築がお済みでない方は、Kerasをインストールしましょう。
では、早速コードを書いていきましょう。まずは、ビットコインとイーサリアムの両通貨のデータへ、close_off_highとvolatilityを追加しましょう。close_off_highは同日のクローズ価格と高値の差を表す指標として追加しています。「-1」の値だと、その日の終値が底値と同じ値という意味です。同様に「1」の場場合は終値が高値と同じ値を表しています。
volatility（ボラティリティ）のカラムは、単純に同日の高値と底値の差額を始値で割った指標です。
|
|
for coins in ['bt_', 'eth_']: kwargs = { coins+'close_off_high': lambda x: 2*(x[coins+'High']- x[coins+'Close'])/(x[coins+'High']-x[coins+'Low'])-1, coins+'volatility': lambda x: (x[coins+'High']- x[coins+'Low'])/(x[coins+'Open'])} market_info = market_info.assign(**kwargs) |
次に、モデルで使わないカラムを削除とデータの並び替え（古い→新しい）のソートをしてあげましょう。
|
|
model_data = market_info[['Date']+[coin+metric for coin in ['bt_', 'eth_'] for metric in ['Close','Volume','close_off_high','volatility']]] # need to reverse the data frame so that subsequent rows represent later timepoints model_data = model_data.sort_values(by='Date') model_data.head() |
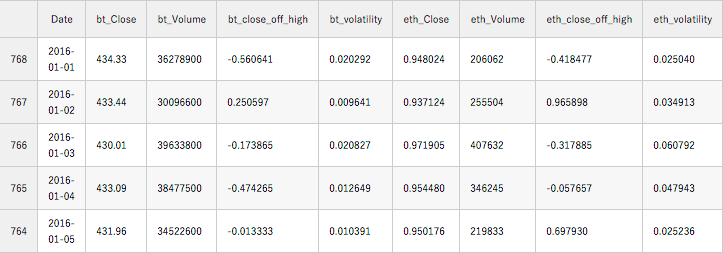
今回構築するLSTMの予測モデルですが、ビットコインとイサーリアムの過去の価格データを学習して、次の日の価格を予測するモデルとなります。予測モデルへ何日前のデータを使うのかを決めなくてはいけません。今回はひとまず「10日」と指定して、予測モデルを構築してみましょう。（この指定する期間も色々と試してみると、より精度の高いモデルが構築可能かと思います）
期間を10日と決めたので、10日間区切りの小さいデータフレーム（window – 「窓」と呼びましょう）を作成していきます。つまり、最初の「窓」はトレーニングセットの最初の0-9行のデータで構成されます。（Pythonは0インデックスを採用しています）。10日間という比較的短い期間で設定をしていることで、より多くの「窓」をモデルに学習させることが可能です。ただし、モデルが長い期間の傾向を理解する材料が少なくなるデメリットもあります。（もし長期間の傾向があるのであれば、の話ですが）
LSTMの期間も決まったので、次はディープラーニングでお決まりのノーマライゼーション（正規化）をしてあげましょう。ディープラーニングのモデルでは、学習するインプットの値が大きく異なることを苦手とします。例えば一つの項目では0< x1 < 10のレンジの値で、違う項目では-100000 < x2 < 1000000と、値の幅が大きいとうまく学習をすることが出来ません。
正規化には色々な手法がありますが、一般的な方法を採用して、値を-1 < x < 1の幅にしてあげましょう。off_highとvolatilityのカラムは大丈夫なので、他のカラムの値を処理してあげます。加えて、日付などのデータは機械学習に使わないのでデータフレームから外しちゃいましょう。
|
|
# dateのカラムを削除 training_set, test_set = model_data[model_data['Date']<split_date], model_data[model_data['Date']>=split_date] training_set = training_set.drop('Date', 1) test_set = test_set.drop('Date', 1) |
|
|
# 「窓」を10日に設定してあげます # 終値と取引量を正規化 window_len = 10 norm_cols = [coin+metric for coin in ['bt_', 'eth_'] for metric in ['Close','Volume']] |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# トレーニングとテストのデータセットを「窓」で分ける LSTM_training_inputs = [] for i in range(len(training_set)-window_len): temp_set = training_set[i:(i+window_len)].copy() for col in norm_cols: temp_set.loc[:, col] = temp_set[col]/temp_set[col].iloc[0] - 1 LSTM_training_inputs.append(temp_set) LSTM_training_outputs = (training_set['eth_Close'][window_len:].values/training_set['eth_Close'][:-window_len].values)-1 LSTM_test_inputs = [] for i in range(len(test_set)-window_len): temp_set = test_set[i:(i+window_len)].copy() for col in norm_cols: temp_set.loc[:, col] = temp_set[col]/temp_set[col].iloc[0] - 1 LSTM_test_inputs.append(temp_set) LSTM_test_outputs = (test_set['eth_Close'][window_len:].values/test_set['eth_Close'][:-window_len].values)-1 #最後にトレーニングのインプットデータを確認してみましょう LSTM_training_inputs[0] |
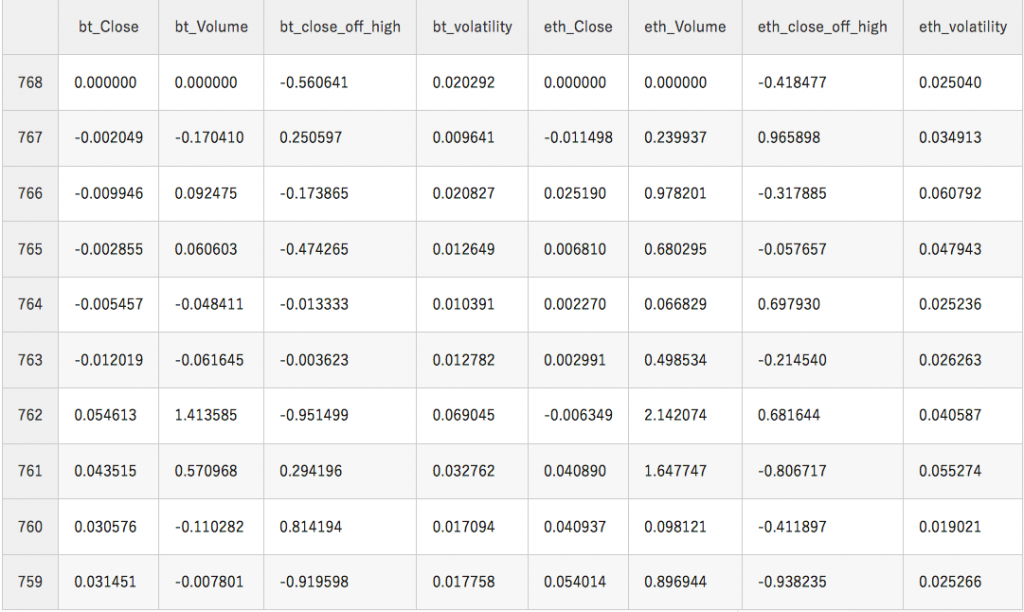
上の表ですが、今回LSTMモデルへ入力するデータの一例となります。表をみると気づくと思いますが、終値(Close）と取引量(Volume)は全データで「0」から始まるようになっています。これで、この10日間での価格の変動幅を予測することが可能です。
データの前処理も終わったので、次はいよいよLSTMのモデルを構築していきましょう！Kerasを使ったことがない方でも、ご安心ください。Kerasですが、本当に驚くほど簡単にディープラーニングのモデルの構築が簡単できるように設計されています。
では、早速Kerasを使ってモデル構築をしてみましょう。
|
|
# PandasのデータフレームからNumpy配列へ変換しましょう LSTM_training_inputs = [np.array(LSTM_training_input) for LSTM_training_input in LSTM_training_inputs] LSTM_training_inputs = np.array(LSTM_training_inputs) LSTM_test_inputs = [np.array(LSTM_test_inputs) for LSTM_test_inputs in LSTM_test_inputs] LSTM_test_inputs = np.array(LSTM_test_inputs) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# Kerasの使用するコンポーネントをインポートしましょう from keras.models import Sequential from keras.layers import Activation, Dense from keras.layers import LSTM from keras.layers import Dropout # いよいよモデル構築です！ def build_model(inputs, output_size, neurons, activ_func="linear", dropout=0.25, loss="mae", optimizer="adam"): model = Sequential() model.add(LSTM(neurons, input_shape=(inputs.shape[1], inputs.shape[2]))) model.add(Dropout(dropout)) model.add(Dense(units=output_size)) model.add(Activation(activ_func)) model.compile(loss=loss, optimizer=optimizer) return model |
上記のようにディープラーニングの各層を宣言するだけで、構築が可能です。コードを見ると解りますが、LSTMの層は今回の入力するデータのサイズをフィットするよう指定されています。また、活性化関数やドロップアウトなどもここで指定しています。（両者とも非常に重要な項目です）
機械学習でイーサリアムの価格を予測してみよう
さて、いよいよデータをインプットしてモデルのトレーニングを始めましょう。LSTMの層で使うニューロンの数ですが、私が使っているパソコンでも早く計算が終わるように今回は20で試して見ましょう。50エポックで私のマシーンで約5分程度かかりました。
まずはイーサリアムからトレーニングして見ましょう。
|
|
# ランダムシードの設定 np.random.seed(202) # 初期モデルの構築 eth_model = build_model(LSTM_training_inputs, output_size=1, neurons = 20) # モデルのアウトプットは次の窓の10番目の価格（正規化されている） LSTM_training_outputs = (training_set['eth_Close'][window_len:].values/training_set['eth_Close'][:-window_len].values)-1 # データを流してフィッティングさせましょう eth_history = eth_model.fit(LSTM_training_inputs, LSTM_training_outputs, epochs=50, batch_size=1, verbose=2, shuffle=True) |
Epoch 1/50
6s – loss: 0.1648
……
Epoch 50/50
4s – loss: 0.0625
50エポック回して、上記の通りしっかりとlossも下がってきています。ちゃんとラーニングしているかどうか、lossとエポックでグラフを確認して見ましょう。
|
|
fig, ax1 = plt.subplots(1,1) ax1.plot(eth_history.epoch, eth_history.history['loss']) ax1.set_title('TrainingError') if eth_model.loss == 'mae': ax1.set_ylabel('Mean Absolute Error (MAE)',fontsize=12) # もでるおんロス計算を変更した場合のため else: ax1.set_ylabel('Model Loss',fontsize=12) ax1.set_xlabel('# Epochs',fontsize=12) plt.show() |
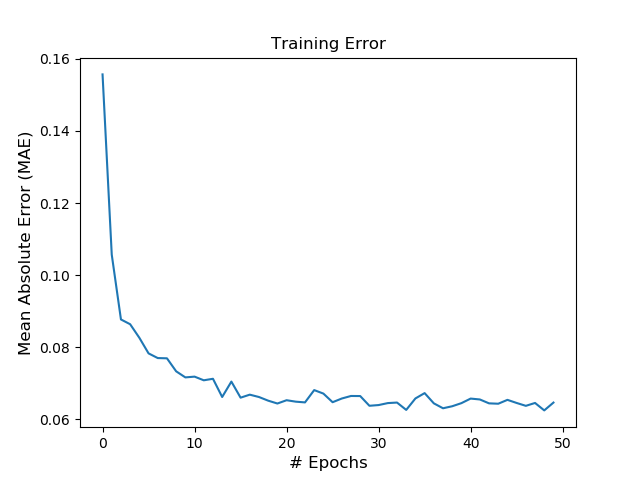
これで、イーサリアムの明日の価格を予測するLSTMモデルの構築が完了しました！ドキドキですね（笑）。では、実際にこの構築したモデルがトレーニングデータセット（2017年10月以前）のデータで、どれくらい予測できているのかを確認して見ましょう。
プロッティングと予測の処理を一緒にしてしまいましょう。また予測値は価格の変動値なので、各日にちの終値に変換する処理も必要です。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes from mpl_toolkits.axes_grid1.inset_locator import mark_inset fig, ax1 = plt.subplots(1,1) ax1.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,5,9]]) ax1.set_xticklabels([datetime.date(i,j,1).strftime('%b %Y') for i in range(2013,2019) for j in [1,5,9]]) ax1.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), training_set['eth_Close'][window_len:], label='Actual') ax1.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), ((np.transpose(eth_model.predict(LSTM_training_inputs))+1) * training_set['eth_Close'].values[:-window_len])[0], label='Predicted') ax1.set_title('Training Set: Single Timepoint Prediction') ax1.set_ylabel('Ethereum Price ($)',fontsize=12) ax1.legend(bbox_to_anchor=(0.15, 1), loc=2, borderaxespad=0., prop={'size': 14}) ax1.annotate('MAE: %.4f'%np.mean(np.abs((np.transpose(eth_model.predict(LSTM_training_inputs))+1)-\ (training_set['eth_Close'].values[window_len:])/(training_set['eth_Close'].values[:-window_len]))), xy=(0.75, 0.9), xycoords='axes fraction', xytext=(0.75, 0.9), textcoords='axes fraction') # 下記コードはこちらのURL参照しました：http://akuederle.com/matplotlib-zoomed-up-inset axins = zoomed_inset_axes(ax1, 3.35, loc=10) axins.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,5,9]]) axins.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), training_set['eth_Close'][window_len:], label='Actual') axins.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), ((np.transpose(eth_model.predict(LSTM_training_inputs))+1) * training_set['eth_Close'].values[:-window_len])[0], label='Predicted') axins.set_xlim([datetime.date(2017, 3, 1), datetime.date(2017, 5, 1)]) axins.set_ylim([10,60]) axins.set_xticklabels('') mark_inset(ax1, axins, loc1=1, loc2=3, fc="none", ec="0.5") plt.show() |
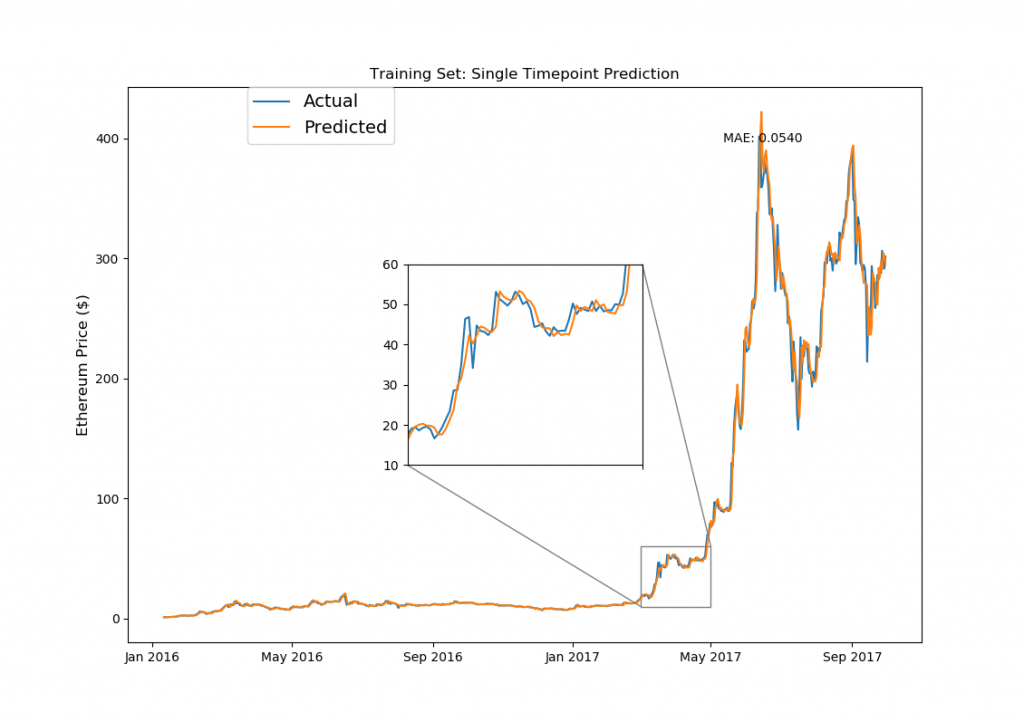
LSTMのモデル構築で使用したトレーニングデータを使っての予測なので、この結果自体は驚くものではありません。上記のモデル構築のコードでドロップアウトを使っていますが、もし使わないで数百個のニューロンで数千回のエポック（反復計算）を行えば、おそらく誤差のない予測も可能です。（いわゆるオーバーフィッティング、日本語で過学習ってやつです）。
では、次が本番です！LSTMのモデルが今まで見たことのないテストの期間（2017年10月移行のデータ）を使って予測をしてみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
fig, ax1 = plt.subplots(1,1) ax1.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax1.set_xticklabels([datetime.date(2017,i+1,1).strftime('%b %d %Y') for i in range(12)]) ax1.plot(model_data[model_data['Date']>= split_date]['Date'][window_len:].astype(datetime.datetime), test_set['eth_Close'][window_len:], label='Actual') ax1.plot(model_data[model_data['Date']>= split_date]['Date'][window_len:].astype(datetime.datetime), ((np.transpose(eth_model.predict(LSTM_test_inputs))+1) * test_set['eth_Close'].values[:-window_len])[0], label='Predicted') ax1.annotate('MAE: %.4f'%np.mean(np.abs((np.transpose(eth_model.predict(LSTM_test_inputs))+1)-\ (test_set['eth_Close'].values[window_len:])/(test_set['eth_Close'].values[:-window_len]))), xy=(0.75, 0.9), xycoords='axes fraction', xytext=(0.75, 0.9), textcoords='axes fraction') ax1.set_title('Test Set: Single Timepoint Prediction',fontsize=13) ax1.set_ylabel('Ethereum Price ($)',fontsize=12) ax1.legend(bbox_to_anchor=(0.1, 1), loc=2, borderaxespad=0., prop={'size': 14}) plt.show() |
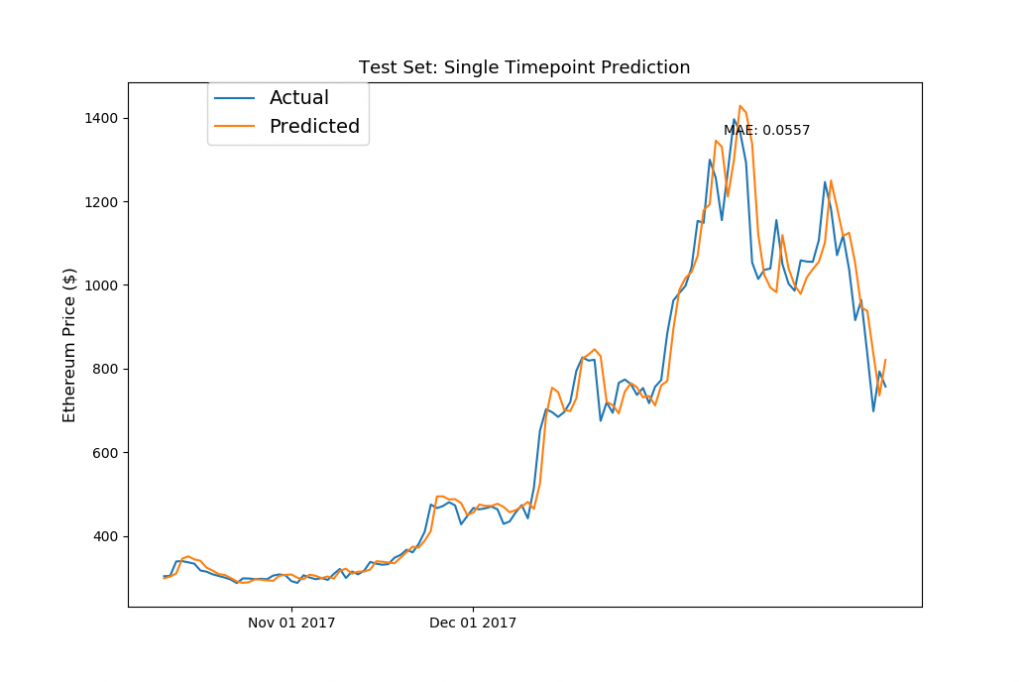
おおお！パッとみた感じは、テストデータでも、想像以上にしっかりと予測ができてそうですが・・このグラフを見ると何か気づきませんか・・？
そうです、LSTMで構築したニュラールネットですが、結果的には本チュートリアルで一番最初にやった「前日の終値を翌日の価格とする」予測と似たような結果になっていますね。
加えて、全体的に「Acutual（実価格）」のラインよりも、「Predict（予測価格）」が上回っているように見えます。つまり、今回構築したLSTMのモデルでは、実価格よりも少し高めで予測してしまっているという訳です。
この誤差ですが、これは恐らくLSTMのトレーニングで使ったデータの価格が要因かと思われます（確定的ではありませんが）。イーサリアムのトレーニングデータですが、価格が劇的に高騰していたので、LSTMのモデルはこれをトレンドとして捉えて、予測値が実価格より全体的に高くなった傾向にあるのかと思われます。
次はビットコインをLSTMで価格予測
イーサリアムでの予測と同じ要領で、まずはトレーニングデータセットでLSTMのモデルを訓練しましょう。モデルの訓練ですが、私の環境で5分程度要しました。
|
|
# ランダムシードの設定 np.random.seed(202) # モデル構成 bt_model = build_model(LSTM_training_inputs, output_size=1, neurons = 20) # トレーニングデータでモデルの訓練（ビットコイン版） bt_history = bt_model.fit(LSTM_training_inputs, (training_set['bt_Close'][window_len:].values/training_set['bt_Close'][:-window_len].values)-1, epochs=50, batch_size=1, verbose=2, shuffle=True) |
Epoch 1/50
– 12s – loss: 0.0967
……
Epoch 50/50
– 13s – loss: 0.0263
ちゃんとイーサリアムと同様にビットコインでもLossがしっかりとエポック毎に減少しているのが確認できますね。続いて、トレーニングデータ（2017年10月以前）で予測を作って、プロッティングしてみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes from mpl_toolkits.axes_grid1.inset_locator import mark_inset fig, ax1 = plt.subplots(1,1) ax1.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,5,9]]) ax1.set_xticklabels([datetime.date(i,j,1).strftime('%b %Y') for i in range(2013,2019) for j in [1,5,9]]) ax1.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), training_set['bt_Close'][window_len:], label='Actual') ax1.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), ((np.transpose(bt_model.predict(LSTM_training_inputs))+1) * training_set['bt_Close'].values[:-window_len])[0], label='Predicted') ax1.set_title('Training Set: Single Timepoint Prediction') ax1.set_ylabel('Bitcoin Price ($)',fontsize=12) ax1.annotate('MAE: %.4f'%np.mean(np.abs((np.transpose(bt_model.predict(LSTM_training_inputs))+1)-\ (training_set['bt_Close'].values[window_len:])/(training_set['bt_Close'].values[:-window_len]))), xy=(0.75, 0.9), xycoords='axes fraction', xytext=(0.75, 0.9), textcoords='axes fraction') ax1.legend(bbox_to_anchor=(0.1, 1), loc=2, borderaxespad=0., prop={'size': 14}) # figure inset code taken from http://akuederle.com/matplotlib-zoomed-up-inset axins = zoomed_inset_axes(ax1, 2.52, loc=10, bbox_to_anchor=(400, 307)) # zoom-factor: 2.52, location: centre axins.set_xticks([datetime.date(i,j,1) for i in range(2013,2019) for j in [1,5,9]]) axins.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), training_set['bt_Close'][window_len:], label='Actual') axins.plot(model_data[model_data['Date']< split_date]['Date'][window_len:].astype(datetime.datetime), ((np.transpose(bt_model.predict(LSTM_training_inputs))+1) * training_set['bt_Close'].values[:-window_len])[0], label='Predicted') axins.set_xlim([datetime.date(2017, 2, 15), datetime.date(2017, 5, 1)]) axins.set_ylim([920, 1400]) axins.set_xticklabels('') mark_inset(ax1, axins, loc1=1, loc2=3, fc="none", ec="0.5") plt.show() |
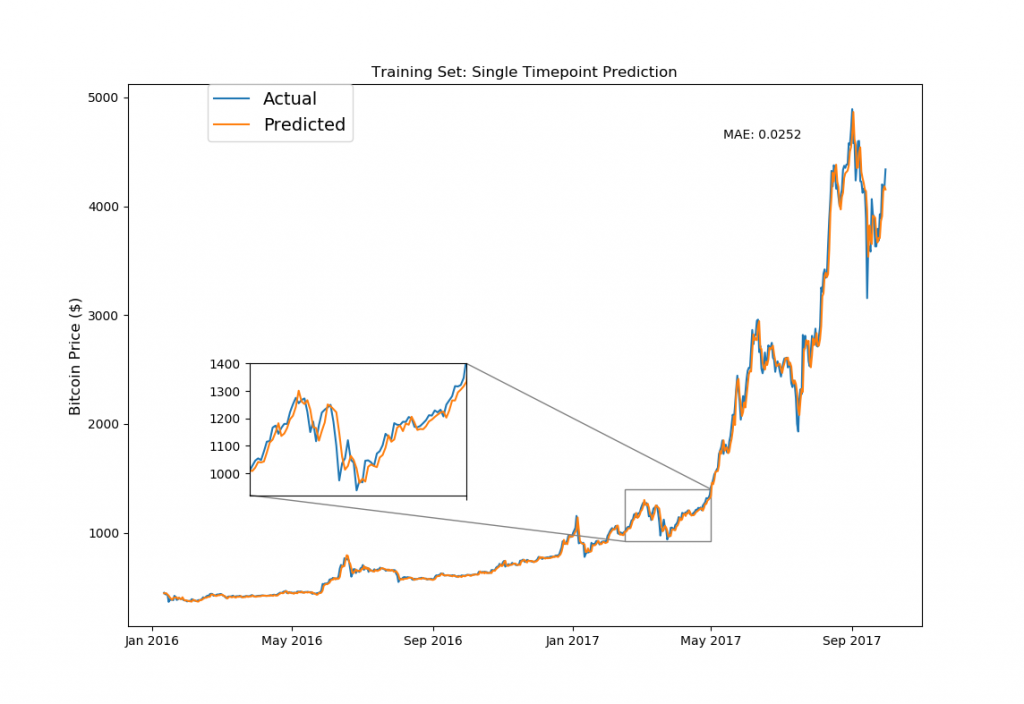
イーサリアムと同様でこちらのプロットは、LSTMに学習させたトレーニングデータを使った予測です。では、まだモデルが見たことの無い全く新しいデータ（つまりテストデータ）を使って予測＆プロッティングして見ましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
fig, ax1 = plt.subplots(1,1) ax1.set_xticks([datetime.date(2017,i+1,1) for i in range(12)]) ax1.set_xticklabels([datetime.date(2017,i+1,1).strftime('%b %d %Y') for i in range(12)]) ax1.plot(model_data[model_data['Date']>= split_date]['Date'][10:].astype(datetime.datetime), test_set['bt_Close'][window_len:], label='Actual') ax1.plot(model_data[model_data['Date']>= split_date]['Date'][10:].astype(datetime.datetime), ((np.transpose(bt_model.predict(LSTM_test_inputs))+1) * test_set['bt_Close'].values[:-window_len])[0], label='Predicted') ax1.annotate('MAE: %.4f'%np.mean(np.abs((np.transpose(bt_model.predict(LSTM_test_inputs))+1)-\ (test_set['bt_Close'].values[window_len:])/(test_set['bt_Close'].values[:-window_len]))), xy=(0.75, 0.9), xycoords='axes fraction', xytext=(0.75, 0.9), textcoords='axes fraction') ax1.set_title('Test Set: Single Timepoint Prediction',fontsize=13) ax1.set_ylabel('Bitcoin Price ($)',fontsize=12) ax1.legend(bbox_to_anchor=(0.1, 1), loc=2, borderaxespad=0., prop={'size': 14}) plt.show() |
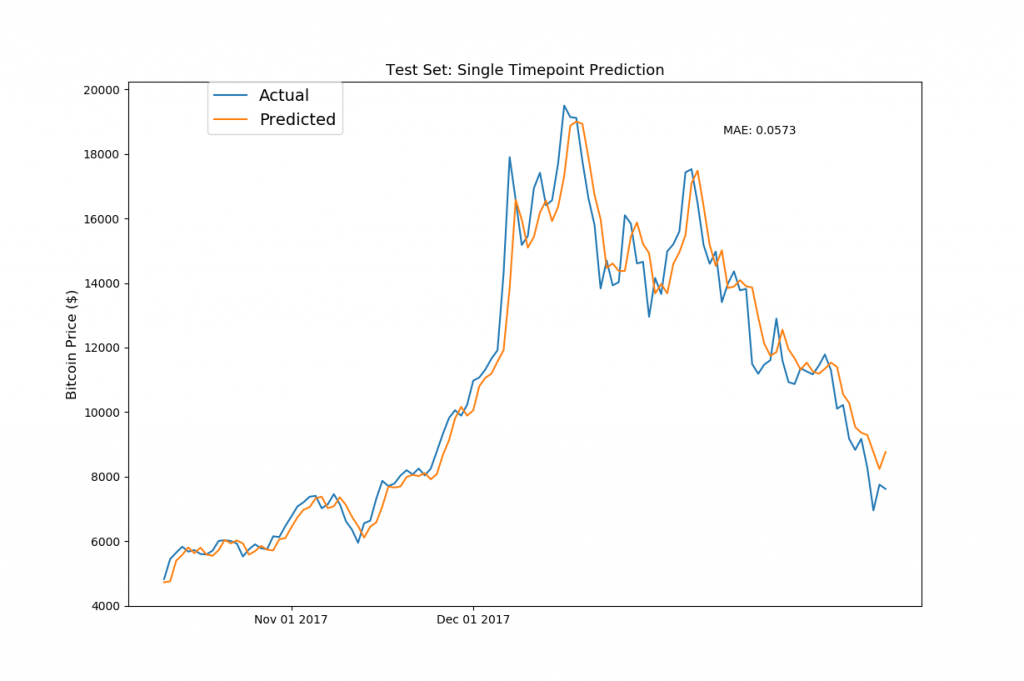
やはりビットコインもイサーリアムと同様で、今回構築したモデルでは前日の終値を次の日の価格として予測している傾向がかなり強いですね。
ディープラーニングのLSTMモデルを使って予測をしましたが、この結果を見てみると「自己回帰モデル（ARモデル）」と似ているのがわかります。自己回帰モデルですが、今回のような仮想通貨や株価などのタイムシリーズ（時系列データ）を予測する際に頻繁に使われるモデルとなります。つまり今回作ったLSTMのモデルは、学習をした結果、異なるモデルと似たような予測方法を取り入れたってことですね。
（それなら・・最初から自己回帰モデルを構築した方が圧倒的に時間の短縮になったじゃん）
LSTMモデルとランダムウォークとの比較をしてみよう
上記で構築したシングルポイントの予測モデルですが、色々と改善する部分はあるものの、予測ラインをざっくり見た感じではそこそこって感じですよね。ただ、「機械学習じゃない予測」でやった、あのつまらない「ランダムウォークモデル」も見た感じは、そこそこ感がありました。
では、最新鋭（？）のニューラルネットワークで予測したモデルと、このランダムウォークのモデルですが、実際にはどちらが、どれくらい優れているのかを比較してみましょう。
ランダムウォークモデルでは乱数シードによって大きく予測精度が変動すると説明しましたが、LSTMモデルでも初期の重みはランダムにアサインされますので、乱数シードによりモデル精度が変動します。
ということで、次はビットコインとイーサリアムで各25個ずつLSTMモデルとランダムウォークモデルを構築して、実際の価格と予想価格の差（絶対値）を比べてみましょう。
下記コードですが、両方の仮想通貨に対して25モデルずつ構築しますので時間が要します！実行する際は気をつけてください。私のMacの環境で10〜15時間程度要しました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# このコードは実行に時間を要しますので気をつけてください # 両仮想通貨で25 LSTMモデルを構築します # h5py経由でモデルを保存します import h5py for rand_seed in range(775,800): print(rand_seed) np.random.seed(rand_seed) temp_model = build_model(LSTM_training_inputs, output_size=1, neurons = 20) temp_model.fit(LSTM_training_inputs, (training_set['eth_Close'][window_len:].values/training_set['eth_Close'][:-window_len].values)-1, epochs=50, batch_size=1, verbose=0, shuffle=True) temp_model.save('eth_model_randseed_%d.h5'%rand_seed) temp_model = build_model(LSTM_training_inputs, output_size=1, neurons = 20) temp_model.fit(LSTM_training_inputs, (training_set['bt_Close'][window_len:].values/training_set['bt_Close'][:-window_len].values)-1, epochs=50, batch_size=1, verbose=0, shuffle=True) temp_model.save('bt_model_randseed_%d.h5'%rand_seed) |
これで両方の仮想通貨でLSTMモデルのフィッティングが完了しましたので、保存した訓練済みモデルを読み込んで、誤差を計算してあげましょう。比較する誤差の指標はMAEを使いましょう。MAEはMean Absolute Error（平均絶対誤差）の意味で、実価格と予測価格の絶対値誤差の平均です。
|
|
# 構築したLSTMモデルのMAEを計算してみましょう from keras.models import load_model eth_preds = [] bt_preds = [] for rand_seed in range(775,800): temp_model = load_model('eth_model_randseed_%d.h5'%rand_seed) eth_preds.append(np.mean(abs(np.transpose(temp_model.predict(LSTM_test_inputs))- (test_set['eth_Close'].values[window_len:]/test_set['eth_Close'].values[:-window_len]-1)))) temp_model = load_model('bt_model_randseed_%d.h5'%rand_seed) bt_preds.append(np.mean(abs(np.transpose(temp_model.predict(LSTM_test_inputs))- (test_set['bt_Close'].values[window_len:]/test_set['bt_Close'].values[:-window_len]-1)))) |
次はLSTMモデルで行った処理を同様にランダムウォークモデルでも行いましょう。
|
|
eth_random_walk_preds = [] bt_random_walk_preds = [] for rand_seed in range(775,800): np.random.seed(rand_seed) eth_random_walk_preds.append( np.mean(np.abs((np.random.normal(eth_r_walk_mean, eth_r_walk_sd, len(test_set)-window_len)+1)- np.array(test_set['eth_Close'][window_len:])/np.array(test_set['eth_Close'][:-window_len])))) bt_random_walk_preds.append( np.mean(np.abs((np.random.normal(bt_r_walk_mean, bt_r_walk_sd, len(test_set)-window_len)+1)- np.array(test_set['bt_Close'][window_len:])/np.array(test_set['bt_Close'][:-window_len])))) |
これで、LSTMモデルとランダムウォークモデルのMAE（実価格と予測価格の絶対値誤差の平均）が算出できましたので、ボックスプロットを使ってグラフにしてみましょう。
|
|
fig, (ax1, ax2) = plt.subplots(1,2) ax1.boxplot([bt_preds, bt_random_walk_preds],widths=0.75) ax1.set_ylim([0, 0.2]) ax2.boxplot([eth_preds, eth_random_walk_preds],widths=0.75) ax2.set_ylim([0, 0.2]) ax1.set_xticklabels(['LSTM', 'Random Walk']) ax2.set_xticklabels(['LSTM', 'Random Walk']) ax1.set_title('Bitcoin Test Set (25 runs)') ax2.set_title('Ethereum Test Set (25 runs)') ax2.set_yticklabels('') ax1.set_ylabel('Mean Absolute Error (MAE)',fontsize=12) plt.show() |
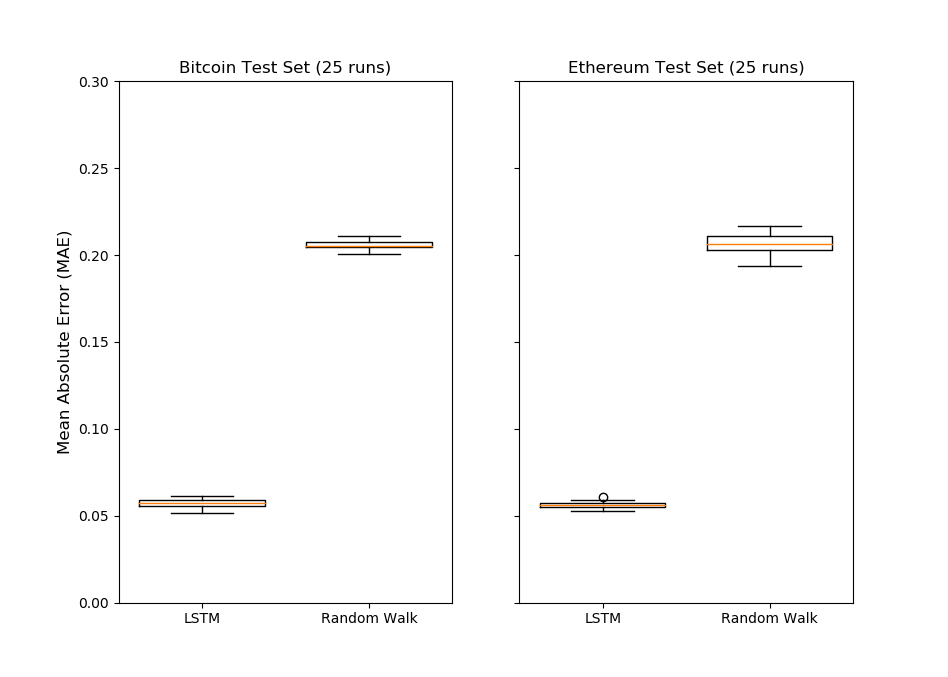
おお！これは嬉しい結果ですね！このプロットで見る限り、人工知能（LSTMモデル）の方が仮想通貨の価格予測をするのに優れているのが解ります！！
と言っても、ランダムウォークモデルよりも優れたモデルを構築するのは、さほど大変ではありません。仮想通貨の価格予測のようなタイムシリーズモデルは他にも多数あります。重み付き平均や自己回帰モデル、さらにはARIMAやFacebookの開発したプロフェット アルゴリズムなどなど。これらの予測モデル手法と比較してみても面白いかもですね。
機械学習で仮想通貨の億り人を目指すには・・
機械学習(LSTM)を使ってビットコインとイサーリアムを予測してみましたが、いかがでしたでしょうか？今回はあくまでも仮想通貨＋機械学習の世界への入門チュートリアルでしたので、ラグモデルとさほど変わらない予測精度ではありました。機械学習を使って、巷で噂の億り人を目指したい・・という方に向けて、今回構築したLSTMモデルの改善案を記載しておきます。
損失関数の改善
今回はMAE（平均絶対誤差）を使いましたが、MSE（Mean Squared Error – 平均二乗誤差）などを使うことで、もっとアグレッシブなモデルを構築することが可能です。タイムシリーズモデルで使用する損失関数には、様々な種類がありますので、色々な関数を試して見ると良いかと思います。
特徴量の改善
特徴量とは予測モデルに学習させるデータです。機械学習ではフューチャー・エンジニアリングと呼ばれていますが、この特徴量を工夫することで、モデルの良し悪しが大きく変わります。今回はビットコインとイーサリアムの過去の価格を中心に予測をしましたが、それ以外で予測に関係のあるデータを加えることで、より精度の高いモデルが構築できます。（とは言え、フューチャー・エンジニアリングはとても難しいですが・・）
以上、「機械学習で仮想通貨 の価格予測をやってみよう！KerasでLSTMモデルを構築してビットコインとイーサリアムの翌日の価格を予測する方法」でした。
今回は入門編として、機械学習＋仮想通貨の予測の基本を行いましたが、また後日に続編も考えています！何か希望の題材がありましたら、コメント欄で教えてください！
