私たちは普段から様々なものを「比較」しています。例えばテストの点数や売り上げなどは、他人の点数や他店舗の売り上げと比較して優劣が決まります。このような時、同じ単位での比較はさほど難しくはありません。しかし、単位が違う時はどうでしょう。平熱と身長を例に挙げてみます。平熱が37.3度の人は「他人と比較して平熱が高い」と言えます。身長が200cmの人は「他人と比較して身長が高い」と言えます。それでは、平熱と身長を比較した時、優劣や大小をつけるとしたらどちらが上なのでしょうか。
多くの特徴量を扱う機械学習では、元の数値のままでは比較が難しい場合が存在します。近年のAIブームにより、機械学習の技術の凄さが報道されていますが、全てにおいて万能ではありません。その能力を最大限発揮するためにはデータに対する前処理が必要になってきます。
本稿では、機械学習の前処理の1つである「正規化」と「標準化」について解説していきます。前半は言葉の意味からライブラリの実装方法まで。後半では実際のデータセットを用いて、正規化や標準化が結果に対してどのような影響を与えるかを解説します。本稿が機械学習をこれから学びたいと思っている方や、初学者の方にとっての参考になれば幸いです。
スケーリングとは
正規化や標準化の内容に入る前に、「スケーリング」という言葉について解説します。スケーリング(Feature Scaling)とは特徴量において値を一定のルールに基づいて一定の範囲に変換する処理のことを指します。本稿では、このスケーリングに含まれる以下の2つの手法について解説していきます。
- 正規化(Normalization)
- 標準化(Standardization)

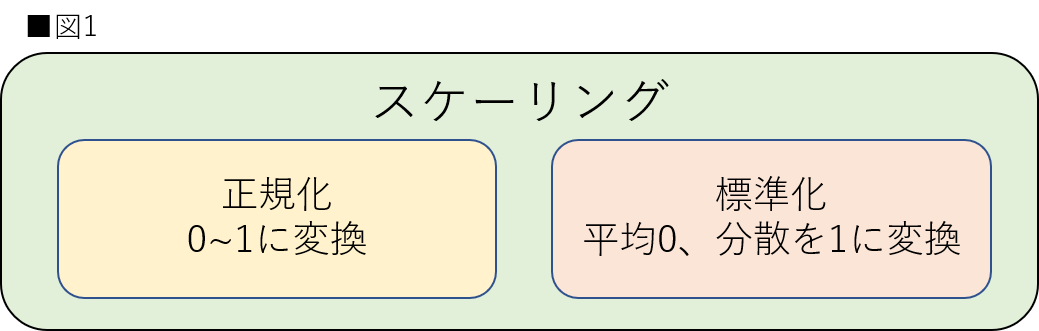
詳細・実装に関しては後述しますが、図1のように本稿での正規化は「特徴量を0〜1に変換するスケーリング」、標準化は「特徴量の平均を0、分散を1に変換するスケーリング」と定義することを先に記載しておきます。これらの言葉の意味は記事や分野によってニュアンスが異なる場合があります。本稿では図1のように定義していますが、絶対ではありません。特に正規化に関しては分野によって言葉の意味が違います。他分野の正規化の意味を調べたい方は、Wikipediaにも分野別に記載されていますので、確認してみてください。(参考:WIkipedia 正規化)
こちらも詳細は後述しますが、スケーリングは全ての機械学習モデルに有効に働くわけではないことに注意してください。そのため、ここからの解説はスケーリングが比較的有効である場合のモデルを前提に進めていきます。
スケーリングの目的①
スケーリングの目的の1つは特徴量がもつ値の重みを平等にするということです。これらはSVM(Support Vector Machine)やkNN(k-Nearest Neighbors)などの特徴量間の距離をベースとしたモデルに有効とされています。機械学習を扱うにおいて特徴量は基本的に数値が使用されます。数値には我々が普段扱うような単位の情報はありません。そのため、モデルは学習時に単位の違う数値同士を同じ尺度で捉えてしまう可能性があります。これを防ぐためにスケーリングは存在します。言葉だけで考えると難しいと感じる方もいらっしゃると思いますので、この後の節では表を用いながらスケーリングを「適応しない場合」と「適応する場合」の比較をしていきます。
スケーリングを適応しない場合
まずは適応しない場合について考えます。表Aには生徒の身体的特徴から機械学習を用いて生徒の体調を予測するときに用意されたデータセットを示しています。こちらはスケーリングを適応する場合でも使用します。
表Aを見てください。生徒ごとの身長と平熱が記載されています。身長と平熱の特徴量を比較してどちらの方が重みが大きいと思うでしょうか。身長は162cm〜182cmの間に収まっていて、平熱は35.6℃〜37.1℃の間に収まっています。どちらも一般的な範囲だと判断できると思います。今回は、この2つの特徴量について比較するためにユークリッド距離を用いて生徒同士の距離を計算してみたいと思います。ユークリッド距離についての詳細な説明は省きますが、基本的には点と点を定規で測った場合の距離と考えていただければ大丈夫です。(参考:WIkipedia:ユークリッド距離)
今回は生徒A-C間、生徒D-E間についてのユークリッド距離を求めます。比較のため、A-C間は身長を固定し、A-D間は平熱を固定します。
A-C間とD-E間のユークリッド距離を見てみると、D-E間のユークリッド距離の方が明らかに大きくなっています。この理由は計算式を見れば明らかです。平熱の数値の幅に比べて身長の数値の幅の方が広くなっているためです。しかし、2つのユークリッド距離には違和感が生じます。平熱での1.5℃の差に対するユークリッド距離が、身長の20cmの差に比べて近すぎます。これは筆者の感覚ですが、平熱が1.5℃違う人を2人探し出すことは、身長が20cm違う2人を探し出すのと同じくらいか、もしくはより難しいと感じます。身長と平熱の値がもつ範囲が一定でないことにより、明らかに身長に対する重みが大きくなっています。このように本来単位が違うはずの特徴量を、同じ尺度で捉えようとすると比較が難しくなる場合があります。機械学習モデルも同様に、学習がうまくいかなくなる可能性があります。
スケーリングを適応した場合
次にスケーリングを適応した場合を考えます。表Bは表Aに対して、標準化のスケーリングを適応した場合の表です。表Bの値は少数第3位まで求めています。
表Bを見ると、標準化によって表Aがスケーリングされています。記載した通り、標準化は各特徴量の平均を0、標準偏差が1になるような分布に変換しています。そのため、同じ特徴量内で元の値が同じであれば、標準化後の値も同じになります。そのため、身長のAとBは「-0.304」、平熱のDとEは「-0.287」で等しいことが表Bから読み取れます。スケーリングを適応していない場合と同様にユークリッド距離を用いて、生徒間の距離を計算します。計算結果を見比べてみましょう。
A-C間とD-E間のユークリッド距離を見てみると、標準化のスケーリングを行わない場合と比較して、ユークリッド距離の差が小さくなっていることが分かります。この数値であれば、身長の20cm差と平熱の1.5℃の比較について、スケーリング前よりも比較的正確に行うことができます。今回は身長と平熱で比較しましたが、さらに数値の差が大きくなるような特徴量同士ではこの問題はより顕著になります。
スケーリングの目的②
スケーリングを行うもう一つの目的は、学習のコストの削減です。これは線形回帰やニューラルネットワークや最急降下法を用いたモデルで有効とされています。特徴量の範囲が異なれば、最急降下時に更新されるパラメーターのサイズが異なってしまします。学習がスムーズに行われるために、スケーリングが必要なのです。最急降下法に関しては数式的な理解が必要になるため、ここでは説明を省きます。
線形回帰や最急降下法についてより詳しく知りたい方はcodexaが提供している下記のコースを参照すると理解が深まります。こちらも避けては通れない内容ですので、理解しておきましょう。本稿に対する理解度もより深まると思います。
スケーリングの影響が少ないモデル
スケーリングが有効なモデルが存在するのに対して、比較的影響を受けにくいモデルも存在します。ランダムフォレストや、LightGBMなどのツリーベース型のモデルです。ツーリーベース型のモデルは各特徴量内の分割を繰り返します。そのため、特徴量同士のスケールを合わせなくても、影響を受けにくくなります。ツリーベース型のモデルの詳細については非常に深い内容となってしまうため、本稿では解説しません。codexaが提供するコースやAIマガジンを参考にしてみてください。
「正規化」と「標準化」の定義と実装
ここまでスケーリングの目的、適応するモデルについて解説してきました。ここからは実際にスケーリング手法の正規化と標準化について、それぞれを解説→実装の順番で記載していきます。後半で実際のデータセットに適応させる際にスムーズに進められるよう、コーディングとライブラリの仕様を詳細に解説します。
本稿はGoogle Colabを用いて実装していきます。2021年7月時点でコードの実行確認を行いましたので、Google Colabのデフォルトのバージョンが変更されない限り、ライブラリをそのままインポートすれば同じように実装可能です。是非、ご自身でも実装してみてください。Google Colabを使用したことがない方は下記の記事を参考にしてください。(参考:Google Colabの知っておくべき使い方 – Google Colaboratoryのメリット・デメリットや基本操作のまとめ)
正規化とは
まずは、正規化(Normalization)について解説していきます。実際には「Normalization」は複数の手法を持ち、本稿で述べている正規化は英語で「min-max normalization」と表記されます。スケーリングの解説時に記載したように、正規化とは各特徴量に対して0〜1に変化する処理のことを指します。各特徴量の取りうる範囲が違ったとしても、正規化によって揃えることができます。正規化についての数式を見て見ましょう。
特徴量内の各値を最小値から引いたものを、特徴量内の最大値から最小値を引いた値で割ることで正規化を行なっています。式自体はシンプルなため、理解自体は難しくないと思います。使用する際の注意点としては、正規化は外れ値に敏感であることです。非常に大きな値や小さな値が外れ値として存在していた場合、他の値が0や1付近に引っ張られます。そのため、正規化を使用する際は外れ値が存在していないかを確認する必要があります。
表Dはスケーリングで使用した表Aに対して、外れ値を付与したものです。表Dと表Eは正規化後の値を示しています。表Dを見てみると生徒Cの身長(10000cm)と生徒Dの平熱(0℃)が外れ値として存在しています。その結果、表Eにおいて身長は0付近に、平熱は1付近に値が引っ張られています。こういった現象が発生するため、正規化を扱う際の外れ値の存在には注意が必要です。
正規化のPython 実装
ここから正規化の実装に入ります。視覚的に正規化による変換を理解するため、ランダムな乱数を発生させ、正規化を行います。正規化の適応部分以外はそこまで重要な内容ではないので詳細な説明は省きますが、乱数の生成や、可視化方法に興味がある方は参考にしてみてください。正規化の実装は下記の流れに沿って行います。「1.scikit-learnによる実装」だけ正規化前後の点をプロットします。
0. 乱数の生成
1. scikit-learnによる正規化の実装(正規化前後のプロットを含む)
2. Numpyによる正規化の実装
3. Pandasによる正規化の実装
0.乱数の生成
まずはNumpyを用いて乱数を発生させます。Pandasでの正規化も実装するので、DataFrame型に変換したものも用意しておきます。
#[IN]:
#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#2次元の乱数の生成
np.random.seed(seed = 0)
data_n = np.random.multivariate_normal([4, 4], [[2, 0], [0, 2]], 200 )
#DataFrame型も用意
data_p = pd.DataFrame(data_n)
#numpyとpandasで頭5行を表示
print("numpyの配列↓")
print(data_n[0:5])
print("pandasのDataFrame↓")
print(data_p.head(5))
#[OUT]:
numpyの配列↓
[[6.49474675 4.56590775]
[5.38414453 7.16910155]
[6.64112584 2.61792037]
[5.34362793 3.78594858]
[3.8540265 4.58067397]]
pandasのDataFrame↓
0 1
0 6.494747 4.565908
1 5.384145 7.169102
2 6.641126 2.617920
3 5.343628 3.785949
4 3.854026 4.580674
スケーリング前とスケーリング後の点を可視化するための関数を定義します。
#[IN]: def image_show(data_beore,data_after,title): #出力サイズ plt.figure(figsize = (8, 8)) #タイトル plt.title(title) #x軸とy軸の範囲を設定 plt.xlim([-8, 8]) plt.ylim([-8, 8]) #目盛の刻み plt.xticks(np.arange(-8, 9, 1)) plt.yticks(np.arange(-8, 9, 1)) #プロットの設定 plt.scatter(data_beore[:, 0], data_beore[:, 1], c='blue', s=10, label='before') plt.scatter(data_after[:, 0], data_after[:, 1], c='red', s=10, label='after') #ラベルの設定 plt.legend(fontsize = 15) #中心ラインの設定 plt.hlines(0, xmin = -8, xmax = 8, linestyles = 'dashed') plt.vlines(0, ymin = -8, ymax = 8, linestyles = 'dashed') plt.show() return
1.scikit-learnによる正規化の実装(正規化前後のプロットを含む)
ここからそれぞれのライブラリ毎に正規化を実装します。最初はscikit-learnのMinMaxScalerクラスを用います。他の手法による正規化の実装と結果を比較するために、正規化後の最初5行を表示します。正規化前後の点も同時にプロットし、正規化前を青、正規化後を赤として表示します。
#[IN]: from sklearn.preprocessing import MinMaxScaler #正規化のクラスを準備 ms = MinMaxScaler() #特徴量の最大値と最小値を計算し変換 data_sc = ms.fit_transform(data_n) #プロット image_show(data_n,data_sc, 'min-max normalization')
#[IN]: #最初5行を提示 print(data_sc[0:5])
#[OUT]: [[0.87722065 0.63085115] [0.7214759 0.9968524 ] [0.89774804 0.35696997] [0.71579408 0.52119123] [0.50690057 0.63292724]]
正規化後の点が赤でプロットされました。この出力を見ても、正規化が0〜1にスケーリングしているのが視覚的に分かると思います。正規化の実装を見てみます。MinMaxScalerクラスを定義した後、メソッドを使用して変換を行います。今回はfit_transform()メソッドを使用しましたが、その他のメソッドについての一部も記載しておきます。
fit() 与えられた特徴量の最大値と最小値を計算する。
fit_transform() 最大値と最小値を計算し、変換する。
inverse_transform() 正規化を元に戻す。
transform() fit()で得られた値を用いて変換する。
適応されたクラスは属性を持ちます。属性が持つ値についても一部表示します。
#[IN]:
print("各特徴量ごとの最小値は"+str(ms.data_min_))
print("各特徴量ごとの最大値は"+str(ms.data_max_))
print("各特徴量ごとの範囲は"+str(ms.data_range_))
print("サンプル数は"+str(ms.n_samples_seen_))
#[OUT]: 各特徴量ごとの最小値は[0.23936256 0.07896172] 各特徴量ごとの最大値は[7.37027566 7.19148898] 各特徴量ごとの範囲は[7.13091311 7.11252726] サンプル数は200
特徴量毎の最小値、最大値、最大値と最小値の幅が表示されました。「1.scikit-learnによる正規化の実装」については以上になります。本稿で解説した部分だけでも十分に扱えるかと思いますが、さらに詳細を知りたい方はscikit-learnの公式ドキュメントを参考にしてみてください。(参考:sklearn.preprocessing.MinMaxScaler)
2.Numpyによる正規化の実装
次にNumpyのメソッドを用いて実装を行なっていきます。乱数に関しては最初に定義したdata_n変数を用います。Numpyのメソッドを用いた実装の場合はscikit-learnとは異なり正規化の計算式を定義してあげる必要があります。今回はmin_max_n()という関数を作成し、正規化後の値を返すようにします。
#[IN]: #正規化を行う関数の定義 def min_max_n(n, axis=None): #最小値の計算 min_n = n.min(axis = axis, keepdims = True) #最大値の計算 max_n = n.max(axis = axis, keepdims = True) #正規化の計算 min_max_n = (n - min_n) / (max_n - min_n) return min_max_n
#[IN]: #最初5行を表示 print(min_max_n(data_n,axis=0)[0:5])
#[OUT]: [[0.87722065 0.63085115] [0.7214759 0.9968524 ] [0.89774804 0.35696997] [0.71579408 0.52119123] [0.50690057 0.63292724]]
「1.scikit-learnによる正規化の実装」と同じ値が出力されています。実装の容易さという点ではscikit-learnを用いた方が簡単だと思います。しかし、実装の内容を知るという点で一度こちらのコードでも実装し理解することをお勧めします。メソッドを使用して計算すると、内部の実装を理解せずに先に進めてしまいます。非常に便利ですが、学習という観点から見ると悪い点でもありますので、可能な限り理解できるように努めましょう。
3.Pandasによる正規化の実装
最後にpandasのメソッドを用いて正規化を実装します。DataFrame型であったとしてもscikit-learnを用いて正規化は実装できます。その際、返り値はNumpyになることに注意してください。「2.Numpyによる正規化の実装」と同様に実装の中身を知るという点でPandasを用いても実装できるようにしておくことをお勧めします。また、Pandasは機械学習を扱う上で必須なライブラリなため、基本的な使い方は押さえておきましょう。min_max_p()という関数を作成し、正規化後の値を返すようにします。
#[IN]: #正規化を行う関数の定義 def min_max_p(p): #最小値の計算 min_p = p.min() #最大値の計算 max_p = p.max() #正規化の計算 min_max_p = (p - min_p) / (max_p - min_p) return min_max_p
#[IN]: #最初5行を表示 print(min_max_p(data_p).head(5))
#[OUT]:
0 1
0 0.877221 0.630851
1 0.721476 0.996852
2 0.897748 0.356970
3 0.715794 0.521191
4 0.506901 0.632927
「1.scikit-learnによる正規化の実装」、「2.Numpyによる正規化の実装」と同じ値が出力されています。これで正規化に関する実装は終わりになります。後半でも正規化を使用する場面があるので、分からない部分がある方は数式と実装を見比べながら確認しておいてください。
標準化とは
次に、標準化(Standardization)について解説していきます。正規化とは異なり、標準化は基本的に平均を0、標準偏差を1にする変換として定義されています。入力の特徴量が正規分布に従うと仮定した変換を行うことができます。標準化を式で表すと下記のようになります。
特徴量内の各値から平均値を引いた値を標準偏差で割ることで標準化を実現します。正規化が0〜1の範囲に収めているのとは異なり、標準化は特定の範囲に収めるような変換ではない点を理解してください。標準化はあくまで、分布内の平均値を0、標準偏差を1にする変換です。
標準化を実装する上で注意する点は、標準偏差(σ)には通常の標準偏差と不偏標準偏差が存在するということです。データには母集団と呼ばれる全体を示すデータと標本と呼ばれる母集団から抽出されたデータがあります。その中で、母集団から求められる分散を母分散、標本から求められる分散を不偏分散と呼びます。この時、統計学的に、不偏分散は母分散よりも少しだけ小さくなることが知られています。そのため、分散の平方根である標準偏差にも若干の違いが生じます。本稿では数式には触れませんが、標準偏差を利用する標準化の実装においてこの2つの違いはとても重要なため、理解しておきましょう。(参考:Wikipedia 標本の標準偏差)
使用するライブラリによって標準偏差のみを実装できるものと、不偏標準偏差も実装できるものに分かれます。表Fに本稿で使用するライブラリ及びメソッドにおける適応を記載しました。
NumpyとPandasでは引数のddofの値を指定することで標準偏差と不偏標準偏差を指定できます。表F内の「標準」は引数を指定しなかった場合を指します。ライブラリによって「標準」の引数が異なるため注意してください。scikit-learnのStandardScalerでは不偏標準偏差を指定することはできません。そのため、標本を用いたデータセットを使用する際はNumpyもしくはPandasを用いて実装する必要があります。
標準化のPython 実装
ここから標準化の実装に入ります。乱数に関しては正規化で作成したものを使用します。標準化の実装は下記の流れで行います。「1.scikit-learnによる標準化の実装」だけ標準化前後の点をプロットします。「2.Numpyによる標準化の実装」、「3.Pandasによる標準化の実装」では標準偏差と不偏標準偏差の両方の場合で結果を出力します。
- sckit-learnによる標準化の実装(正規化前後のプロットを含む)
- Numpyによる標準化の実装
- Pandasによる標準化の実装
1.sckit-learnによる標準化の実装(標準化前後のプロットを含む)
乱数は生成してあるため、標準化の定義から行います。
#[IN]: from sklearn.preprocessing import StandardScaler # 標準化のクラスを定義 ms = StandardScaler() #fit_transformを用いて、特徴量の平均値と標準化を計算してから特徴量のスケール変換を行う data_std = ms.fit_transform(data_n) #プロットを定義 image_show(data_n,data_std, 'Standardization')
#[IN]: #最初5行を表示 print(data_std[0:5])
#[OUT]: [[ 1.8438581 0.39370492] [ 1.0552128 2.27487202] [ 1.94780276 -1.01398504] [ 1.02644172 -0.16992331] [-0.03133318 0.40437555]]
標準化後の点が赤でプロットされました。この出力を見ても、標準化が0付近に分布しているのが視覚的に分かると思います。グラフからも分かるように標準化は特定の範囲に収める変換ではありません。正規化の時と同様に、その他のメソッドについての一部も記載します。
fit() 与えられた特徴量の平均値と標準偏差を計算する。
fit_transform() 平均値と標準偏差を計算し、変換する。
inverse_transform() 標準化を元に戻す。
transform() fit()で得られた値を用いて変換する。
適応されたクラスは属性を持ちます。属性が持つ値についても一部表示します。
#[IN]:
print("各特徴量ごとの平均値は"+str(ms.mean_))
print("各特徴量ごとの標準偏差は"+str(ms.var_))
print("サンプル数は"+str(ms.n_samples_seen_))
#[OUT]: 各特徴量ごとの平均値は[3.89815116 4.02109161] 各特徴量ごとの標準偏差は[1.98314123 1.9149536 ] サンプル数は200
「1.scikit-learnによる標準化の実装」については以上になります。正規化と同様にscikit-learnは便利ですが、内部の仕様を理解せずに使用することはお勧めしません。scikit-learnの公式ドキュメントもあるため、詳細な変数などはこちらでも確認しておきましょう。(参考:sklearn.preprocessing.StandardScaler)
2.Numpyによる標準化の実装
次にNumpyのメソッド用いて実装を行なっていきます。Numpyのメソッドを用いた実装の場合はscikit-learnとは違い標準化の計算式を定義してあげる必要があります。今回はstandard_n()という関数を作成し、正規化後の値を返すようにします。
#[IN]: def standard_n(n, axis = None, ddof = 0): #平均値を計算 mean_n = n.mean(axis = axis, keepdims = True) #標準偏差を計算 ddof=0なら標準偏差、ddof=1なら不偏標準偏差 std_n = n.std(axis = axis, keepdims = True, ddof = ddof) #標準化の計算 standard_n = (n - mean_n) / std_n return standard_n
#[IN]:
print("標準化【標準偏差】↓")
print(standard_n(data_n,0,0)[0:5])
print("標準化【不偏標準偏差】↓")
print(standard_n(data_n,0,1)[0:5])
#[OUT]: 標準化【標準偏差】↓ [[ 1.8438581 0.39370492] [ 1.0552128 2.27487202] [ 1.94780276 -1.01398504] [ 1.02644172 -0.16992331] [-0.03133318 0.40437555]] 標準化【不偏標準偏差】↓ [[ 1.83924267 0.39271942] [ 1.05257146 2.26917771] [ 1.94292715 -1.0114469 ] [ 1.0238724 -0.16949797] [-0.03125475 0.40336335]]
標準偏差を用いた標準化の出力結果が「1.scikit-leanによる標準化の実装」と一致しました。不偏標準偏差を使用した標準化の出力については次の「3.Pandasによる標準化の実装」と比較します。計算式で難しい部分はありませんが、平均と標準偏差を求める際にkeepdims引数にTrueを渡しています。これは配列の次元数を落とさずに結果を求めるための引数です。慣れていない方には少し難しく感じるかもしれません。下記の記事を参考にしてみてください。(参考:NumPy♪関数maxやsumにおけるkeepdims指定の図解)
3.Pandasによる標準化の実装
最後にPandasのメソッドを用いて標準化を実装します。こちらも正規化と同様にDataFrame型であったとしてもscikit-learnを用いて正規化は実装できます。その際、返り値はNumpyになることも同様です。standard_p()という関数を作成し、正規化後の値を返すようにします。この関数の返り値はDataFrame型のままになります。
#[IN]: #標準化を行う関数の定義 def standard_p(p, ddof = 1): #最小値の計算 mean_p = p.mean() #最大値の計算 std_p = p.std(ddof = ddof) #標準化の計算 standard_p = (p - mean_p) / (std_p) return standard_p
#[IN]:
print("標準化【標準偏差】↓")
print(standard_p(data_p,ddof=0).head(5))
print("標準化【不偏標準偏差】↓")
print(standard_p(data_p,ddof=1).head(5))
#[OUT]:
標準化【標準偏差】↓
0 1
0 1.843858 0.393705
1 1.055213 2.274872
2 1.947803 -1.013985
3 1.026442 -0.169923
4 -0.031333 0.404376
標準化【不偏標準偏差】↓
0 1
0 1.839243 0.392719
1 1.052571 2.269178
2 1.942927 -1.011447
3 1.023872 -0.169498
4 -0.031255 0.403363
標準偏差を用いた標準化の結果が「1.scikit-learnによる標準化の実装」、「2.Numpyによる標準化の実装」と同じ値が出力されています。不偏標準偏差を用いた標準化も同様に、「2.Numpyによる標準化の実装」と同じ値が出力されています。若干数値が違う箇所に関しては表示されている桁数の影響であるため問題ありません。標準化の実装については以上になります。後半の実装でも標準化は登場するので、しっかりと理解しておいてください。
正規化と標準化のどちらを使用するべきか
正規化と標準化についてある程度理解できたかと思いますが、どちらを使用するべきか疑問に思う方もいるのではないでしょうか。この問題に関しては、使用するモデルや精度と比較しながら検討することであるため、一概に決めることはできません。例えば正規化は外れ値に敏感であると述べましたが、外れ値が存在するというだけで使用しないわけではありません。外れ値を除外すれば当然正規化を用いることができる場合もあります。
こういった判断は知識と経験の積み重ねで実現されます。与えられた課題に対して今までの経験や知識から、どちらを使用するべきか判断するという場合が多いです。難しいと感じるかもしれませんが、色々なデータセットで試してみながら知見を深めることが重要です。本稿も活用しながら少しづつ学習を進めていきましょう。
正規化・標準化を用いたワインの分類
本節ではscikit-learnを用いて利用できるワイン認識のデータセットを用いて機械学習における分類問題を実装します。本稿での実装では主に正規化と標準化を適応する場合と適応しない場合の比較を中心に行います。EDAなどは詳細には行いません。EDAなどについて知りたい方はAIマガジンの【データサイエンティスト入門編】探索的データ解析(EDA)の基礎操作をPythonを使ってやってみようを参考にしてみてください。
正規化と標準化の解説時にライブラリがインポートされているかもしれませんが、この節ではもう一度使用するライブラリをインポートし直します。ここから先のコードだけでもワインの分類は行うことができます。
#[IN]:
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
ワインデータの読み込みを行います。ワインデータの基礎知識は下記の通りです。
- ワインのデータ数→178
- ワインの種類→3クラス(class_0(59)、class_1(71)、class_2(48) )
- 各特徴量
- Alcohol:アルコール
- Malic acid:リンゴ酸
- Ash:灰分
- Alcalinity of ash:灰分のアルカリ性
- Magnesium:マグネシウム
- Total phenols:全フェノール
- Flavanoids:フラボノイド
- Nonflavanoid phenols:非フラバノイドフェノール類
- Proanthocyanins:プロアントシアニン
- Color intensity:色彩強度
- Hue:色調
- OD280/OD315 of diluted wines:蒸留ワインのOD280/OD315
- Proline:プロリン
#[IN]: from sklearn.datasets import load_wine #ワインのデータセットを読み込み data_wine = load_wine() data_wine
#[OUT]:
{'DESCR': '.. _wine_dataset:\n\nWine recognition dataset\n------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 178 (50 in each of three classes)\n :Number of Attributes: 13 numeric, predictive attributes and the class\n :Attribute Information:\n \t\t- Alcohol\n \t\t- Malic acid\n \t\t- Ash\n\t\t- Alcalinity of ash \n \t\t- Magnesium\n\t\t- Total phenols\n \t\t- Flavanoids\n \t\t- Nonflavanoid phenols\n \t\t- Proanthocyanins\n\t\t- Color intensity\n \t\t- Hue\n \t\t- OD280/OD315 of diluted wines\n \t\t- Proline\n\n - class:\n - class_0\n - class_1\n - class_2\n\t\t\n :Summary Statistics:\n \n ============================= ==== ===== ======= =====\n Min Max Mean SD\n ============================= ==== ===== ======= =====\n Alcohol: 11.0 14.8 13.0 0.8\n Malic Acid: 0.74 5.80 2.34 1.12\n Ash: 1.36 3.23 2.36 0.27\n Alcalinity of Ash: 10.6 30.0 19.5 3.3\n Magnesium: 70.0 162.0 99.7 14.3\n Total Phenols: 0.98 3.88 2.29 0.63\n Flavanoids: 0.34 5.08 2.03 1.00\n Nonflavanoid Phenols: 0.13 0.66 0.36 0.12\n Proanthocyanins: 0.41 3.58 1.59 0.57\n Colour Intensity: 1.3 13.0 5.1 2.3\n Hue: 0.48 1.71 0.96 0.23\n OD280/OD315 of diluted wines: 1.27 4.00 2.61 0.71\n Proline: 278 1680 746 315\n ============================= ==== ===== ======= =====\n\n :Missing Attribute Values: None\n :Class Distribution: class_0 (59), class_1 (71), class_2 (48)\n :Creator: R.A. Fisher\n :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)\n :Date: July, 1988\n\nThis is a copy of UCI ML Wine recognition datasets.\nhttps://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data\n\nThe data is the results of a chemical analysis of wines grown in the same\nregion in Italy by three different cultivators. There are thirteen different\nmeasurements taken for different constituents found in the three types of\nwine.\n\nOriginal Owners: \n\nForina, M. et al, PARVUS - \nAn Extendible Package for Data Exploration, Classification and Correlation. \nInstitute of Pharmaceutical and Food Analysis and Technologies,\nVia Brigata Salerno, 16147 Genoa, Italy.\n\nCitation:\n\nLichman, M. (2013). UCI Machine Learning Repository\n[https://archive.ics.uci.edu/ml]. Irvine, CA: University of California,\nSchool of Information and Computer Science. \n\n.. topic:: References\n\n (1) S. Aeberhard, D. Coomans and O. de Vel, \n Comparison of Classifiers in High Dimensional Settings, \n Tech. Rep. no. 92-02, (1992), Dept. of Computer Science and Dept. of \n Mathematics and Statistics, James Cook University of North Queensland. \n (Also submitted to Technometrics). \n\n The data was used with many others for comparing various \n classifiers. The classes are separable, though only RDA \n has achieved 100% correct classification. \n (RDA : 100%, QDA 99.4%, LDA 98.9%, 1NN 96.1% (z-transformed data)) \n (All results using the leave-one-out technique) \n\n (2) S. Aeberhard, D. Coomans and O. de Vel, \n "THE CLASSIFICATION PERFORMANCE OF RDA" \n Tech. Rep. no. 92-01, (1992), Dept. of Computer Science and Dept. of \n Mathematics and Statistics, James Cook University of North Queensland. \n (Also submitted to Journal of Chemometrics).\n',
'data': array([[1.423e+01, 1.710e+00, 2.430e+00, ..., 1.040e+00, 3.920e+00,
1.065e+03],
[1.320e+01, 1.780e+00, 2.140e+00, ..., 1.050e+00, 3.400e+00,
1.050e+03],
[1.316e+01, 2.360e+00, 2.670e+00, ..., 1.030e+00, 3.170e+00,
1.185e+03],
...,
[1.327e+01, 4.280e+00, 2.260e+00, ..., 5.900e-01, 1.560e+00,
8.350e+02],
[1.317e+01, 2.590e+00, 2.370e+00, ..., 6.000e-01, 1.620e+00,
8.400e+02],
[1.413e+01, 4.100e+00, 2.740e+00, ..., 6.100e-01, 1.600e+00,
5.600e+02]]),
'feature_names': ['alcohol',
'malic_acid',
'ash',
'alcalinity_of_ash',
'magnesium',
'total_phenols',
'flavanoids',
'nonflavanoid_phenols',
'proanthocyanins',
'color_intensity',
'hue',
'od280/od315_of_diluted_wines',
'proline'],
'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2]),
'target_names': array(['class_0', 'class_1', 'class_2'], dtype='<U7')}
ワインのデータセットを読み込むことができました。Pandasを用いて予測に必要なラベルを抽出します。
#[IN]: #ワインラベルの抽出 df_label = pd.DataFrame(data_wine["target"], columns=["wine"]) #先頭5行を表示 df_label.head()
次に各特徴量もラベルと同様にDataFrame型にして抽出します。
#[IN]: #各特徴量を抽出 df_data = pd.DataFrame(data_wine["data"], columns = data_wine["feature_names"]) #先頭5行を表示 df_data.head()
各特徴量の値が表示されました。このワインのデータセットは訓練データと検証用データに分かれていません。そのため、2分割する必要があります。このデータセットは初学者向けで、比較的簡単な部類に入ります。そのため、本稿では半分を訓練用、もう半分を検証用データとして扱いたいと思います。分割する際ですが、ワインのラベルの割合を等しくするため、stratify引数でラベルを指定します。この引数は他のデータセットを用いる際にも便利なので覚えておくことをお勧めします。
#[IN]: from sklearn.model_selection import train_test_split train_x, test_x, train_y, test_y = train_test_split(df_data, df_label, test_size=0.5,stratify=df_label["wine"],random_state=0)
訓練用と検証用に特徴量と各ラベルを分割できました。ここから正規化と標準化の実装に移ります。まずは正規化と標準化のクラスを定義します。scikit-learnを用いて実装します。
#[IN]: from sklearn.preprocessing import StandardScaler,MinMaxScaler #正規化のクラスを生成 mmsc=MinMaxScaler() #標準化のクラスを生成 stdsc = StandardScaler()
データセットに正規化や標準化を適応する際に1つ注意点があります。訓練データと検証データに適用するクラスは同じものを使用してください。別々にfit()やfit_transform()メソッドを用いると、正規化や標準化の計算条件が異なってしまう可能性があります。そのため、訓練用データでfit()やfit_transform()メソッドを用いて正規化や標準化のパラメータを計算し、検証用データにはtransform()メソッドを用いてスケーリングを行いましょう。スケーリング後の値に関して確認したい方はコメントアウト「#」を外していただければ表示されます。
#[IN]: #注意 #→訓練データでfitした変換器を用いて検証データを変換すること #訓練用のデータを正規化 train_mm = mmsc.fit_transform(train_x) #訓練用のデータを標準化 train_std = stdsc.fit_transform(train_x) #訓練用データを基にテストデータを正規化 test_mm=mmsc.transform(test_x) #訓練用データを基にテストデータを標準化 test_std = stdsc.transform(test_x) #コメントアウトを外すとスケーリング後の値を確認できる #print(train_mm) #print(train_std) #print(test_mm) #print(test_std)
これで準備は整いました。今回は機械学習モデルの定番である「K近傍法」「パーセプトロン」「ランダムフォレスト」を用いて、「元のデータ」「正規化したデータ」「標準化したデータ」の正解率を比較します。
- K近傍法
- パーセプトロン
- ランダムフォレスト
1.K近傍法
最初のモデルはK近傍法です。K近傍法に関する詳細な説明は省きますが、簡単に解説すると「新しいサンプルと特徴が似ているいくつかのサンプルのラベルを参考にして、新しいサンプルのラベルを予測する分類手法」です。具体的にどのようなアルゴリズムになっているか理解したい方は下記のサイトを参考に調べてみてください。(参考:Wikipedia K近傍法)
K近傍法を定義し学習させます。パラメータにはデフォルトの値を用います。デフォルトでは新しいサンプルから近い5個のラベルを用いて判定します。K近傍法に関する詳細な解説はscikit-learnの公式ドキュメントを参考にしてください。(参考:sklearn.neighbors.KNeighborsClassifier)
各データ用にK近傍法を定義し、データを適用します。
#[IN]: from sklearn.neighbors import KNeighborsClassifier #元のデータ用 lr = KNeighborsClassifier() #正規化したデータ用 lr_mm = KNeighborsClassifier() #標準化したデータ用 lr_std = KNeighborsClassifier() #元のデータの適用 lr.fit(train_x, train_y) #正規化したデータの適用 lr_mm.fit(train_mm, train_y) #標準化したデータの適用 lr_std.fit(train_std, train_y)
#[OUT]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
各データの予測結果を求め、正解率を出力します。score()メソッドは正解率(Accurcy)を返します。評価指標に関しては機械学習の評価指標 分類編:適合率や再現率、AUC(ROC曲線、PR曲線)を解説に詳細に記載されています。
#[IN]:
print('元のデータのスコア :',lr.score(test_x, test_y))
print('正規化したデータのスコア :',lr_mm.score(test_mm, test_y))
print('標準化したデータのスコア :',lr_std.score(test_std, test_y))
#[OUT]: 元のデータのスコア : 0.7752808988764045 正規化したデータのスコア : 0.9662921348314607 標準化したデータのスコア : 0.9662921348314607
それぞれの正解率が表示されました。出力を見比べると元のデータのスコアだけが低く、正規化や標準化を行なったデータに対する正解率は0.9を超えています。このことから正規化や標準化がK近傍法に有効であることが分かります。
2.パーセプトロン
次にニューラルネットワークの基礎でもあるパーセプトロンを用いてワインの分類を行います。K近傍法と同様にモデルのパラメータはデフォルトに設定されているものを使用します。パーセプトロンは最近の機械学習分野において必須とも言える知識なので、確実に押さえておきましょう。パーセプトロンやニューラルネットワークについての知識はAIマガジンの今時のエンジニアが知っておくべきディープラーニングの基礎知識を参考にしてみてください。また、scikit-learnのパーセプトロンの引数については公式ドキュメントを参考にしてください。(参考:sklearn.linear_model.Perceptron)
各データ用にパーセプトロンを定義し、データを適用します。
#[IN]: from sklearn.linear_model import Perceptron #元のデータ用 lr = Perceptron(random_state = 0) #正規化したデータ用 lr_mm = Perceptron(random_state = 0) #標準化したデータ用 lr_std = Perceptron(random_state = 0) #元のデータの適用 lr.fit(train_x, train_y) #正規化したデータの適用 lr_mm.fit(train_mm, train_y) #標準化したデータの適用 lr_std.fit(train_std, train_y)
#[OUT]:
Perceptron(alpha=0.0001, class_weight=None, early_stopping=False, eta0=1.0,
fit_intercept=True, max_iter=1000, n_iter_no_change=5, n_jobs=None,
penalty=None, random_state=0, shuffle=True, tol=0.001,
validation_fraction=0.1, verbose=0, warm_start=False)
K近傍法と同様に正解率を出力します。
#[IN]:
print('元のデータのスコア :',lr.score(test_x, test_y))
print('標準化したデータのスコア :',lr_std.score(test_std, test_y))
print('正規化したデータのスコア :',lr_mm.score(test_mm, test_y))
#[OUT]: 元のデータのスコア : 0.5280898876404494 標準化したデータのスコア : 0.9887640449438202 正規化したデータのスコア : 0.9775280898876404
それぞれの正解率が表示されました。元のデータに対する正解率を見ると、K近傍法よりもさらに低くなっています。もとの正規化や標準化を行なったデータに対する正解率は0.9を超えています。このことから正規化や標準化がパーセプトロンに有効であることが分かります。
3.ランダムフォレスト
最後にツリーベース型のモデルであるランダムフォレストを用いてワインの分類を行います。スケーリングの解説で、ツリーベース型のモデルは正規化や標準化にそれほど影響されにくいと記載しました。どの程度の違いに収まるのか、ここで検証していきます。
各データ用にランダムフォレストを定義し、データを適用します。
#[IN]: from sklearn.ensemble import RandomForestClassifier #元のデータ用 lr = RandomForestClassifier(random_state = 0) #正規化したデータ用 lr_mm = RandomForestClassifier(random_state = 0) #標準化したデータ用 lr_std = RandomForestClassifier(random_state = 0) #元のデータの適用 lr.fit(train_x, train_y) #正規化したデータの適用 lr_mm.fit(train_mm, train_y) #標準化したデータの適用 lr_std.fit(train_std, train_y)
#[OUT]:
RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=None, max_features='auto',
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=None, oob_score=False, random_state=0, verbose=0,
warm_start=False)
K近傍法やパーセプトロンと同様に正解率を出力します。
#[IN]:
print('元データのスコア :',lr.score(test_x, test_y))
print('正規化データのスコア :',lr_mm.score(test_mm, test_y))
print('標準化データのスコア :',lr_std.score(test_std, test_y))
#[OUT]: 元データのスコア : 0.9887640449438202 正規化データのスコア : 0.9887640449438202 標準化データのスコア : 0.9887640449438202
それぞれの正解率が表示されました。全てのデータに対しての正解率は0.9台と非常に高く、値もほぼ等しくなっています。この結果からツリーベース型のモデルがスケーリングの影響を受けにくいことがご理解いただけたと思います。
| K近傍法 | 元データ | 0.7752808988764045 |
| 正規化 | 0.9662921348314607 | |
| 標準化 | 0.9662921348314607 | |
| パーセプトロン | 元データ | 0.5280898876404494 |
| 正規化 | 0.9887640449438202 | |
| 標準化 | 0.9775280898876404 | |
| ランダムフォレスト | 元データ | 0.9887640449438202 |
| 正規化 | 0.9887640449438202 | |
| 標準化 | 0.9887640449438202 |
モデルによってスケーリングの影響は様々です。そのため、様々なモデルに対して、スケーリングを行い評価を比較してみることをお勧めします。scikit-leanに用意されているデータセットは比較的簡単に分類できるため初学者の方にも扱いやすいと思います。もう少し難しいデータセットを扱いたい方はkaggleなどのコンペティションに参加してみてください。(参考:sklearn.datasets: Datasets・kaggle)
まとめ
正規化・標準化に関する解説と実装は以上です。モデルやデータセットによって手法が変わるので、難しく感じるかもしれませんが機械学習の面白さはそこにあると筆者は思います。本稿が少しでも皆様の学習の参考になれば幸いです。
codexaでは初学者や独学者向けに機械学習のコースを提供しています。ライブラリや統計的知識、モデルのアルゴリズムに興味がある方は是非受講してみてください。お待ちしております。