データを扱っていると想定外の値を目にすることがあります。筆者も毎日の体重を体重計からスマートフォンに転送し記録していますが、体重計の故障などによって普段であれば考えられない体重が記録されていることがあります。正直、サービスの利用者からすれば、意味のない値は削除してほしいものです。
機械学習の分野でも通常時のデータから外れた値というのはよく目にします。膨大なデータが求められる機械学習ですが、量が多くなればなるほど、誤差やミスなどが発生する確率は高くなります。シンプルに考えるのであれば、除去を行えば問題ないのかもしれません。しかし、データ分析を行うに当たって安易に値を削除することは重要な事態を引き起こす可能性があります。
本稿では機械学習でよく耳にする「外れ値」について解説していきます。その後、Pythonを使用して外れ値の検出方法を実装していきます。機械学習を勉強し始めた方や、データサイエンティストを目指されている人にとって非常に重要な内容のため、しっかりと押さえましょう。
外れ値と異常値
本節では、外れ値と異常値について詳しく解説していきます。これらの言葉の概念は最も初歩的ですが、理解していないと先に進むことができません。図を用いながら可能な限り直感的に、正しく理解できるように解説して行きます。
外れ値とは
外れ値(outlier)とは測定された値の中で他のデータとかけ離れているものを指します。実験結果を記録している中で、他のデータの分布とは明らかに異なる場所に数値が出現したりする際に外れ値と呼ばれることが多いです。外れ値が発生する原因は様々ですが、そのままにしておくと、データ分析の際に統計指標を歪める可能性があるため、何らかの対処が必要な場合があります。図1と図2のグラフは外れ値が存在する典型的な例です。
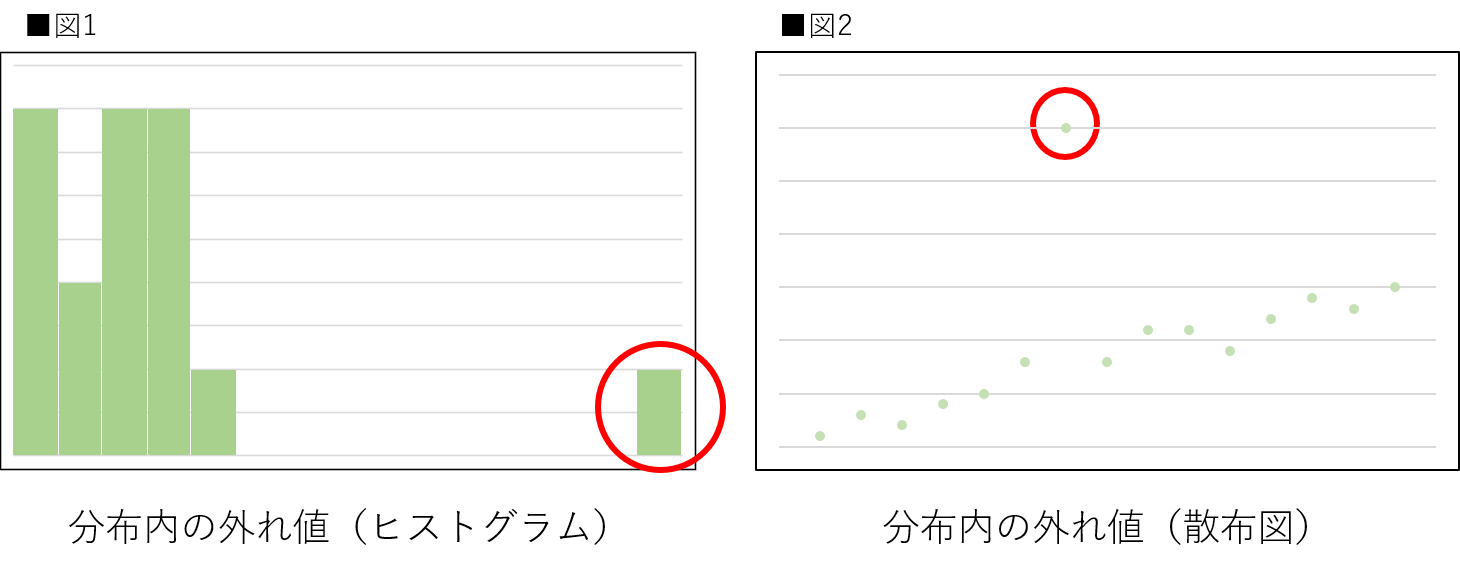
図1と図2を見てみましょう。図1がヒストグラムで図2が散布図です。赤い丸で囲われた部分の値が他のデータとは異なる位置に存在していることが見て取れると思います。どちらも軸の単位が記載されていないため厳密に外れ値と断定できないという話はありますが、ここでは直感的に理解できるように外れ値として扱います。
異常値とは
多くの文献で、外れ値と並んで紹介されるのが、異常値です。外れ値の一種と表現されることもありますが、言葉が持つ意味としては異なります。異常値は外れ値の中で入力ミスや測定ミス等が原因となっているものを指します。つまり、物理的にとりうるはずがない値ということです。例えばものの数を測定するときには、通常は0もしくは正の値しかとりません。その中で負の値を持ったデータがあるなど、とりうるはずのない値が異常値として判定されます。表Aのような倉庫内の製品と在庫数の関係を例にして異常値を確認して見ましょう。
表Aを見て見ましょう。製品「D」が-12個という値を取っています。在庫数のカウントにおいて値が負の数をとることはまずありません。そのため、製品「D」の-12という値は外れ値であり、異常値として扱うことができます。当然、この値を無視することはできません。異常値である以上何らかの処理を行い対処する必要があります。
外れ値が及ぼす影響
前節で外れ値と異常値について解説しました。本節では、外れ値が実際に及ぼす影響について解説していきます。当然ですがデータセットによって外れ値がもたらす影響は異なります。ここでは人為的に作成したデータで欠損値の影響を再現しますが、実際には使用しているデータセット毎に考えなければならないことを理解しておいてください。影響の例としては以下などが挙げられます。
- 外れ値による統計指標の歪み
- 作業コストの増加
- データ分析の精度の低下 など
このような影響を外れ値は及ぼします。もう少し詳細に理解するために、次は実際の数値を使用して見ていきます。
外れ値が及ぼす影響(1次元)
外れ値は統計指標を歪ませる場合があると説明しました。通常のデータとはかけ離れた位置に存在している数値の存在により、数値の平均や標準偏差に影響を与える場合があります。まずは理解しやすい1次元のデータを示します。表Bと表Cはあるクラスの生徒の身長をまとめたものです。2つの表を見比べて何が起こっているかを確認してみます。
表Bと表Cを見比べると、表Cには外れ値が存在し、生徒「G」の値が明らかに不自然なことがわかります。表Bを確認してみると本来の値は「152cm」であったことがわかります。つまり、何かしらの要因により身長がメートルで記載されてしまったと考えられます。ちなみに「1.52cm」の身長の生徒が存在する確率は限りなく0です。そのため、人的ミスであることが確認できればほぼ「異常値」として断定していいと言えます。
次は平均に注目します。外れ値がない場合は「165.80」ですが、外れ値がある場合は「150.75」になっています。これが統計指標の歪みです。今回は生徒の人数が10人だけであるため、影響がかなり大きくで出ています。正しいデータの数がもっと多ければ、外れ値から受ける影響も少なくなりますが、それでも外れ値が表Cにとって悪影響であることは間違いありません。
外れ値が及ぼす影響(2次元)
2次元についても解説していきます。機械学習の分野は多次元データから予測することがほとんどですが、2次元の方が視覚的に理解しやすいため解説ではそちらを使用します。異なる点は次元数ですが、そこまで大きな違いがあるわけではありません。そのため、今回の解説が多次元でも同様に発生すると考えていただくと、理解しやすいと思います。図3、図4ではある企業での20歳〜40歳までの年齢(歳)と平均年収(万円)の相関が高いと仮定したプロットに、近似直線を描画しています。2つの図を見比べて何が起こっているかを確認していきます。
図3と図4を見比べると、外れ値がない場合は年齢が上がるにつれて平均年収も高いことがわかります。しかし、外れ値がある場合はどうでしょうか。21歳の平均年収が1500万になっているだけで、その他の値は全て同じに設定されています。しかし、近似的には年齢が上がるにつれて平均年収が下がると読み取ることができます。このように2次元でも外れ値は全体のデータに影響を与える場合があります。多次元の場合も同様で外れ値に対して全体のデータが引っ張られる場合があります。
大きな影響を与えている21歳の平均年収ですが、この外れ値の原因を少し考えています。例としては以下のようなことが挙げられます。
- 入力を間違えたことによる人的ミス
- 本当に対象企業の21歳の平均年収が1500万である など
このように、外れ値に対しては色々な考えを挙げることができます。外れ値の確かな原因が不明なときは仮説を立ててデータ分析を進めていく必要もあります。ただデータを全体的に眺めて流すのではなく、データが持つ意味を考えながら外れ値に対応していくことが重要です。
外れ値の検出方法
ここまで、外れ値の基本的な概要について解説してきました。ここからは実際に外れ値の検出方法について解説していきます。一概に外れ値の検出方法と言っても様々な手法があります。重要なことはデータセットに合わせた正しい手法の選択と、正しい外れ値を検出できることです。本説では1次元と多次元の場合に分けて解説します。
1次元のデータの場合
最初に1次元データの時の外れ値の検出方法です。外れ値の検出法の中では最も基礎となる部分です。多次元データだとしても、1次元ずつ外れ値を見ていくこともできます。汎用性が高いというメリットがあるため、初学者の方もしっかりと理解しておきましょう。
四分位範囲(IQR)と箱ひげ図
最初に四分位範囲と箱ひげ図について解説していきます。2つの概念には繋がりがあるため、その部分に注目しながら見ていきます。
1.四分位範囲
「四分位範囲(Interquartile range)」とはデータの広がり具合を示す指標の1つで、英名を略してIQRとも呼ばれます。四分位範囲は四分位数を使って求められます。四分位数は、データの値を小さい順に並べた時にデータを4つに分割する時の区切り値のことを指します。小さい順に第1四分位数(Q1)、第2四分位数(Q2)、第3四分位数(Q3)となり、第2四分位数はデータ全体の中央値を指します。第1四分位数と第3四分位数は、第2四分位数と最大値・最小値の範囲内の中央値を指します。四分位範囲の求め方は以下の通りです。前節で用いた表Cを小さい順に整頓したものを利用して表Dとして表示します。
四分位範囲(IQR) = 第3四分位数(Q3) ー 第1四分位数(Q1)
四分位範囲を使って外れ値を検出できます。一般的に、四分位範囲を1.5倍に拡大し、そこから外れる値を外れ値とします。四分位範囲における外れ値は以下の式で表されます。四分位範囲と同じように前節で用いた表を利用して外れ値を計算し、表示します。
外れ値 < 第1四分位数 ー (1.5 × 四分位範囲)
外れ値 > 第3四分位数 + (1.5 × 四分位範囲)
外れ値 < 151.5 (151.5 = 162 ー 1.5 × 7)
外れ値 > 179.5 (179.5 = 169 + 1.5 × 7)
外れ値の求め方について理解できたでしょうか。上の計算結果であれば外れ値は「G」の1.52になります。四分位範囲を使用して外れ値を検出することができました。次はこの四分位範囲から求めた外れ値を可視化できる箱ひげ図について解説していきます。
2.箱ひげ図
箱ひげ図(box-and-whisker plot)は外れ値を可視化する際に非常に便利な図です。四分位範数を含めたデータの要約統計量を確認できます。
箱ひげ図はデータの四分位数と最大値、最小値を表示してくれます。最大値、最小値、外れ値の表示に関しては、箱ひげ図の設定によって異なり、上記に述べたような四分位範囲の1.5倍の範囲で表示することもあれば、外れ値を表示せずに、単にデータ全体の最大値と最小値を表示することもできます。図5では、この後の実装で外れ値を表示することになるので、外れ値を記載しました。
四分位範囲を用いた外れ値検出は、過程となる確率分布がありません。そのため、比較的、汎用性が高いという利点があります。また、他のデータの箱ひげ図と並べた時にデータのばらつきを簡単に可視化できます。しかし、データの数が少なかったりすると外れ値の検出がうまくいかない場合もあるため、注意が必要です。
zスコア
zスコア(z-score)はそれぞれのデータの点数を平均値を0、標準偏差を1になるように変換した値のことです。これによりデータ内の相対的な位置を知ることができます。zスコアによる外れ値検出は有意水準によって決定されます。有意水準が-2と2であれば、外れ値でないデータは95.45%の中に含まれることになり、-3と3では99.73%の中に含まれることになります。また、有意水準の基準については下記の通りです。より詳細に有意水準を決めたい方は正規分布について調べて見てください。箱ひげ図と同様に、前節でも利用した表Dを用いてzスコアによる外れ値を検出します。(参考:Wikipedia 正規分布)
| 有意水準 | 信頼度 |
| <-1.65 かつ +1.65< | 90% |
| <-1.96 かつ +1.96< | 95% |
| <-2 かつ +2< | 95.44% |
| <-2.58 かつ +2.58< | 99% |
| <-3 かつ +3< | 99.73% |
生徒Gのzスコアは-2.98でした。有意水準が2であれば外れ値と判定できます。zスコアを用いた外れ値の検出には似たものとしてスミルノフ・グラブス検定も存在します。部分的には同じですが、スミルノフ・グラブス検定は有意水準の求め方が決まっており、再帰的に行うという特徴があります。(参考:Wikipedia スミルノフ・グラブス検定)
注意点として、zスコアを使用した検定は、データ全体が正規分布に従っていることを仮定としている点を理解しておいてください。データの形状が正規分布に従わない場合、外れ値検出がうまく行かない場合が存在します。そのため、対数変換をすることでデータの分布の形状を変化させる必要があったりもします。この内容に触れると解説が長くなってしまうため、本稿では省きます。しかし、機械学習の分野では重要な内容のため、興味がある方は調べてみてください。
トリム平均
トリム平均とはデータ全体の最大値と最小値から一定の割合だけ削除し、残ったデータで計算した平均です。例えばデータの両側5%を削除した場合は「5%トリム平均」と言います。ここでも先ほどまでと同じ表Dを用いてトリム平均について解説していきます。
表Fは小さい順に並べたデータの両側から10%ずつを削除し、10%トリム平均を求めたものです。削除後の平均が本来の平均値(165.80)に近づきました。実際は、データ全体の20%を削除するようなことは、非常に稀です。今回は元からのデータ数が10個であることと分かりやすいことに重きを置いたことでこのような結果になっています。トリム平均は対象の値が有効かどうかの検証は行いません。実装は非常に簡単ですが、むやみに使用すると外れ値でない値まで削除する可能性があるため、注意が必要です。
多次元データの場合
次に多次元データに対する外れ値の検出方法です。1次元と比較して複雑なものも多いですが少しずつ理解していきましょう。
最初に多次元で外れ値を検出する必要性について解説します。機械学習では基本的に多次元データから予測を立てることが多いです。1次元の外れ値検出では検出できない分布の例は複数存在します。図6ではその1例を示した2次元のを示しています。
図6は分布の真ん中に正しい値を取り、周囲に外れ値が存在してしまっている場合の分布です。このような分布の場合、x軸、もしくはy軸単体でデータを確認しても外れ値を検出できなくなってしまいます。そのため、2次元や多次元のまま外れ値を検出する必要があります。次に、多次元データに使用できる外れ値の検出方法の解説に移ります。ここではscikit-learnで紹介されている外れ値検出の方法を取り上げます。多次元の外れ値検出の方法は他にも多く存在します。興味がある方は本稿で取り上げた以外のものについても調べてみてください。(参考:2.7. Novelty and Outlier Detection)
Isolation Forest
Isolation Forestは決定木を用いた外れ値検出です。与えられたデータ全体から特徴をランダムに選択し、その特徴の中の最大値と最小値の範囲から分割値を選択します。外れ値が存在していた場合、その部分の決定木の深さは他のノードまでの深さに比べて短くなります。Pythonでの実装の際には様々なパラメーターが用意されているので、確認してみてください。(参考:sklearn.ensemble.IsolationForest)
LocalOutlierFactor(LOF)
LOFは値に対する密度を用いた外れ値検出です。データ内のそれぞれの点から近くのk個までの値に対する局所密度を求め、比較します。外れ値が存在していた場合他の点が持つ局所密度よりも、密度が低くなります。これにより、外れ値を検出することができます。k個の値に関しては、実装の段階で指定することができます。(参考:sklearn.neighbors.LocalOutlierFactor)
OneClassSVM (OCSVM)
OCSVMはSVMの概念を利用した外れ値検出です。公式によると、本来OCSVMはパラメータの値によって外れ値検出に有用な結果をもたらす可能性があると述べられており、本来は新規性の検出に最適であると述べています。元々、OCSVMは外れ値に非常に影響を受けやすく、訓練用データに外れ値が潜んでいた場合、良い結果を得ることができません。正しい値を原点から遠くに、外れ値を原点付近に分布させるような特徴空間に写像させることにより外れ値を検出できます。写像の際に使用するカーネルなどは実装の際に選択できます。有効なカーネルを選択するためにもパラメータの確認は必須です。(参考:sklearn.svm.OneClassSVM)
EllipticEnvelope
EllipticEnvelopeはデータ全体が正規分布に従っていると仮定し、楕円を検出します。正規分布を仮定しているため、従わないデータセットに関しては検出がうまくいきません。それでも、1次元のデータの時にも述べたように、正規分布に近づける手段は存在するので組み合わせながら実装していくことをオススメします。(参考:sklearn.covariance.EllipticEnvelope)
これらの手法をおもちゃのデータセットを例に適用し、比較したものも公開されています。手法ごとのメリットとデメリットを把握するためにも、確認しておきましょう。(参考:Comparing anomaly detection algorithms for outlier detection on toy datasets)
外れ値に対する考え方
ここまで、外れ値の概要から検出方法まで解説してきました。ここまで理解した上で本節では改めて外れ値に対する考え方・向き合い方について筆者の意見も含めながら解説していきます。
異常値であるかを検討する
異常値であるかはしっかりと検討する必要があります。明らかに単位が違っていたり、絶対に取り得るはずのない数値であれば異常値と判断する場合もあるかもしれませんが、実際のデータセットで分析者が独断で異常値と判断するのは慎重にならなければなりません。データ分析者とデータ収集者が別の場合、情報の差し違いなどにより、誤認してしまう可能性があります。「この異常値と思われる値はなぜ発生したのか」という理由まで確認した上で異常値と判断することが必要です。
外れ値の除外は慎重に
機械学習を始めたばかりの方の多くは線形回帰やランダムフォレストなどのモデル構築から勉強していく場合が多いです。それは決して悪いことではありません。しかし、モデルの精度を上げることだけを目的とするとデータセット内の邪魔な値(外れ値含む)を極力無くし、汎用的なモデルを作成する方に考えをつぎ込みがちです。kaggleなどのデータ分析コンペティションにおいては単純にスコアを競う場合もあるため、推奨される場合もありますが、現実問題では慎重に考える必要もあります。
時に外れ値というのは、それ自体が必要な情報である場合もあります。例えば工場などにおける異常検知などでは、エラー時の値というのが外れ値として記録されたりもします。外れ値(以上検知時の値)を排除して作成した機械学習モデルは通常の作業においては高い精度を出力できるモデルになりますが、異常検知という動作に関しては全くの無意味になる可能性があります。また、上記の図のようにデータ分析者が安易に外れ値を除外することで本来の目的を達成できない可能性もあります。そのため、外れ値への対応は目的と照らし合わせた上でしっかりと検討することが重要です。
外れ値検出の実装
本節では、外れ値検出をGoogle Colabを用いて実装していきます。本稿は2021年5月時点でコードの実行確認を行いましたので、Google Colabのデフォルトのバージョンが変更されない限り、ライブラリをそのままインポートすれば同じように実装可能です。是非、ご自身でも実装してみてください。(参考:Google Colabの知っておくべき使い方 – Google Colaboratoryのメリット・デメリットや基本操作のまとめ)
外れ値検出は主に1次元データに対応したものを中心に行なっていきます。多次元データの外れ値検出は直感的に理解しにくいため、本稿では散布図を用いて外れ値を可視化するところだけを行います。実際に多次元データから外れ値を検出されたい方はkaggleなどのコンペティションなどを活用しながら、色々なデータセットで試して見てください。(参考:kaggle)
まずは必要なライブラリをインポートします。
#[IN]: #ライブラリの読み込み import numpy as np import pandas as pd import copy import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline
今回使用するのはアヤメのデータセットです。アヤメのデータセットに関する基本情報は以下の通りです。また、AIマガジンでも【データサイエンティスト入門編】探索的データ解析(EDA)の基礎操作をPythonを使ってやってみようでアヤメのデータセットを扱っています。アヤメのデータセットの扱いが初めての方は、こちらも参考にしてみてください。
アヤメのデータセットのカラム名
- sepal_length(がく片の長さ cm)
- sepal_width(がく片の幅 cm)
- petal_length(花びらの長さ cm)
- petal_width(花びらの幅 cm)
- species(花の種類 setosa,versicolor,virginica)
データセットを読み込みます。今回はseabornに用意されているデータセットを利用して実装を行います。ロードと花の種類の表示、データセットの先頭を表示します。(参考:seaborn)
#[IN]:
#アヤメのデータセットの読み込みと表示
df = sns.load_dataset("iris")
print(df.head())
#花の種類を表示
print("花の種類は"+str(df["species"].unique())+"です")
データを可視化
早速、データ全体を可視化してみます。今回はsearbornのpairplotを用いて花の種類ごとに色を分けた散布図とヒストグラムを表示します。非常に簡単に実装できるため、汎用性の高い可視化方法です。他にもseaborn 徹底入門!Pythonを使って手軽で綺麗なデータ可視化8連発で、seabornの可視化方法を取り上げています。参考にしてみてください。
#[IN]: #花の種類(species)ごとに散布図を表示 sns.pairplot(df, hue='species', palette="husl")
特徴量同士の散布図が表示されました。この散布図だけを見るだけでも、少し外れ値と思われる点を見つけることができると思います。このように散布図は2変数間の関係を俯瞰的に可視化できます。ライブラリによる外れ値検出も重要ですが、視覚的に外れ値を確認することも極めて重要です。
箱ひげ図
まずはアヤメのデータセットの特徴量の中から、それぞれ外れ値を検出してみたいと思います。今後何度も箱ひげ図は表示することになるため、get_box()関数を定義して箱ひげ図を表示できるようにします。詳細に関しては省きますが、pandasのplot(“kind”=box)を用いて箱ひげ図を表示しています。
#[IN]:
#箱ひげ図を表示するための関数を定義
def get_box(input_df):
#入力のコピーを作成
output_df=input_df.copy()
#表示する図のサイズを指定
fig = plt.figure(figsize=(20,20))
#箱ひげ図で表示するデータの列を指定
num_list=["sepal_length","sepal_width","petal_length","petal_width"]
#指定した列分繰り返す
for i in range(len(num_list)):
#1出力に複数の図を表示できるように設定
plt.subplot(len(num_list), 4, i+1)
#箱ひげ図の表示
output_df[num_list[i]].plot(kind="box")
return output_df
まずは花の種類を気にせずに外れ値を検出していきたいと思います。特に処理を行わず、最初に作成したデータフームをget_box()関数に引数として与えます。
#[IN]: #sepal_length、sepal_width、petal_length、petal_widthのそれぞれの列から箱ひげ図を表示 df=get_box(df)
箱ひげ図を表示することができました。どうやらsepal_widthの外れ値を検出したようです。しかし、可視化することができただけで、外れ値の正確な情報が不明なため、詳細な情報を得るためにbox_Outlier()関数を定義します。この関数では箱ひげ図のそれぞれの四分位数の情報、外れ値の値とindex値を取得します。実際に上に表示されている箱ひげ図の情報を取得して見ます。
#[IN]:
#四分位数と外れ値のindex値を取得する関数を定義
def box_Outlier(input_df):
#入力のコピーを作成
output_df=input_df.copy()
#詳細を表示するデータの列を指定
num_list=["sepal_length","sepal_width","petal_length","petal_width"]
#指定した列分繰り返す
for i in range(len(num_list)):
#第1四分位数を取得
q1=output_df[num_list[i]].quantile(0.25)
#第2四分位数を取得
q3=output_df[num_list[i]].quantile(0.75)
#IQRを取得
iqr=q3-q1
#外れ値基準の下限を取得
bottom=q1-(1.5*iqr)
#外れ値基準の上限を取得
up=q3+(1.5*iqr)
#列名、Q1、Q3、IQR、外れ値を表示
print(str(num_list[i]))
print("Q1は:"+str(q1))
print("Q3は:"+str(q3))
print("IQRは:"+str(iqr))
print("外れ値は↓")
print(output_df[num_list[i]][(output_df[num_list[i]] < bottom) | (output_df[num_list[i]] > up) ])
print("*********************")
return output_df
#[IN]: #箱ひげ図の詳細を取得 df=box_Outlier(df)
#[OUT]: sepal_length Q1は:5.1 Q3は:6.4 IQRは:1.3000000000000007 外れ値は↓ Series([], Name: sepal_length, dtype: float64) ********************* sepal_width Q1は:2.8 Q3は:3.3 IQRは:0.5 外れ値は↓ 15 4.4 32 4.1 33 4.2 60 2.0 Name: sepal_width, dtype: float64 ********************* petal_length Q1は:1.6 Q3は:5.1 IQRは:3.4999999999999996 外れ値は↓ Series([], Name: petal_length, dtype: float64) ********************* petal_width Q1は:0.3 Q3は:1.8 IQRは:1.5 外れ値は↓ Series([], Name: petal_width, dtype: float64) *********************
箱ひげ図について詳細な情報を取得することができました。sepal_widthに存在した外れ値とindex値が取得できています。情報が取得できたので、これらの値を使用して、データフレームから削除することも可能ですし、他の値で埋めることもできます。当然、有効な対処をしなければならないことは忘れないようにしてください。
ここまで、検出してきたのはアヤメの種類については考えない場合の外れ値でした。しかし、この外れ値の検出方法は本当に正しいのでしょうか。もう一度、最初から考えてみたいと思います。
今回の目的はアヤメのデータセットの中から外れ値を検出することにあります。その上でアヤメの種類は3種類存在しています。つまり、3種類をまとめたデータから外れ値を検出することは有効でない可能性があります。3種類それぞれに特徴が存在しているわけですから、種類毎に外れ値を検出した方が有効的なのではないかと考えることができます。そこで、3種類のアヤメそれぞれに対して箱ひげ図と詳細な情報を出力してみます。先ほどの箱ひげ図と比較して見てください。まずはsetasaにの箱ひげ図について表示して行きます。
#[IN]:
#setosaが含まれるデータのみを抜き出す
setosa_df=df.groupby('species').get_group("setosa")
#setosaのデータに対する箱ひげ図を表示
setosa_df=get_box(setosa_df)
種類ごとに表示される前には現れていなかったpetal_lengthとpetal_widthにも外れ値が存在しています。このように注目するポイントを変えることで、あらたな外れ値が出現することもあります。データセットによってどのように注目点を変えるかは異なりますが、仮説を立てながらデータの味方を変えることは重要です。setosaについての四分位数についての情報も表示します。
#[IN]: #setosaのデータに対する箱ひげ図の詳細を表示 setosa_df=box_Outlier(setosa_df)
#[OUT]: sepal_length Q1は:4.8 Q3は:5.2 IQRは:0.40000000000000036 外れ値は↓ Series([], Name: sepal_length, dtype: float64) ********************* sepal_width Q1は:3.2 Q3は:3.6750000000000003 IQRは:0.4750000000000001 外れ値は↓ 15 4.4 41 2.3 Name: sepal_width, dtype: float64 ********************* petal_length Q1は:1.4 Q3は:1.5750000000000002 IQRは:0.17500000000000027 外れ値は↓ 13 1.1 22 1.0 24 1.9 44 1.9 Name: petal_length, dtype: float64 ********************* petal_width Q1は:0.2 Q3は:0.3 IQRは:0.09999999999999998 外れ値は↓ 23 0.5 43 0.6 Name: petal_width, dtype: float64 *********************
setosaの外れ値はsepal_lengthに0個、sepal_widthに2個、petal_lengthに4個、petal_widthに2個検出されたことがわかりました。次はversicolorについての外れ値を検出して詳細を表示して見ます。
#[IN]:
#versicolorが含まれるデータのみを抜き出す
versicolor_df=df.groupby('species').get_group("versicolor")
#versicolorのデータに対する箱ひげ図を表示
versicolor_df=get_box(versicolor_df)
#[IN]: #versicolorのデータに対する箱ひげ図の詳細を表示 versicolor_df=box_Outlier(versicolor_df)
#[OUT]: sepal_length Q1は:5.6 Q3は:6.3 IQRは:0.7000000000000002 外れ値は↓ Series([], Name: sepal_length, dtype: float64) ********************* sepal_width Q1は:2.525 Q3は:3.0 IQRは:0.4750000000000001 外れ値は↓ Series([], Name: sepal_width, dtype: float64) ********************* petal_length Q1は:4.0 Q3は:4.6 IQRは:0.5999999999999996 外れ値は↓ 98 3.0 Name: petal_length, dtype: float64 ********************* petal_width Q1は:1.2 Q3は:1.5 IQRは:0.30000000000000004 外れ値は↓ Series([], Name: petal_width, dtype: float64) *********************
versicolorの外れ値はsepal_lengthに0個、sepal_widthに0個、petal_lengthに1個、petal_widthに0個検出されたことがわかりました。versicolorにはそれほど外れ値はないようです。次はvirginicaについての外れ値を検出して詳細を表示して見ます。
#[IN]:
#virginicaが含まれるデータのみを抜き出す
virginica_df=df.groupby('species').get_group("virginica")
#virginicaのデータに対する箱ひげ図を表示
virginica_df=get_box(virginica_df)
#[IN]: #virginicaのデータに対する箱ひげ図の詳細を表示 virginica_df=box_Outlier(virginica_df)
#[OUT]: sepal_length Q1は:6.2250000000000005 Q3は:6.9 IQRは:0.6749999999999998 外れ値は↓ 106 4.9 Name: sepal_length, dtype: float64 ********************* sepal_width Q1は:2.8 Q3は:3.1750000000000003 IQRは:0.37500000000000044 外れ値は↓ 117 3.8 119 2.2 131 3.8 Name: sepal_width, dtype: float64 ********************* petal_length Q1は:5.1 Q3は:5.875000000000001 IQRは:0.7750000000000012 外れ値は↓ Series([], Name: petal_length, dtype: float64) ********************* petal_width Q1は:1.8 Q3は:2.3 IQRは:0.4999999999999998 外れ値は↓ Series([], Name: petal_width, dtype: float64) *********************
virginicaの外れ値はsepal_lengthに1個、sepal_widthに3個、petal_lengthに0個、petal_widthに0個検出されたことがわかりました。箱ひげ図による外れ値検出は以上になります。アヤメのデータセットでは種類ごとに50個ずつのデータが存在します。これは機械学習の分野では決して多い量ではありません。この後、外れ値として検出された値を全て除外するのも一つの手ではありますが、全体の分布を見ながら検討する必要があることを忘れないでください。
zスコア
ここまでは箱ひげ図を用いて外れ値検出を行ってきました。ここからはzスコアを用いて外れ値検出を行います。zスコアは正規分布を過程としているため、アヤメの種類ごとにデータをヒストグラムで表示して見たいと思います。ヒストグラム表示のための関数をget_hist()として定義します。
#[IN]:
#ヒストグラムを作成するための関数を定義
def get_hist(input_df):
#入力のコピーを作成
output_df=input_df.copy()
#表示する図のサイズを指定
fig = plt.figure(figsize=(20,20))
#詳細を表示するデータの列を指定
num_list=["sepal_length","sepal_width","petal_length","petal_width"]
#指定した列分繰り返す
for i in range(len(num_list)):
#1出力に複数の図を表示できるように設定
plt.subplot(len(num_list), 4, i+1)
#ヒストグラムの表示
output_df[num_list[i]].plot.hist(bins=15)
return output_df
setosa、versicolor、virginicaについてのヒストグラムを順番に表示します。
#[IN]: #setosaのデータに対するヒストグラムを表示 setosa_df=get_hist(setosa_df)
#[IN]: #versicolorのデータに対するヒストグラムを表示 versicolor_df=get_hist(versicolor_df)
#[IN]: #virginicaのデータに対するヒストグラムを表示 virginica_df=get_hist(virginica_df)
それぞれのヒストグラムを表示することはできました。どのグラフも正規分布に完全に合致という訳ではないですが、極端に違う分布もないため、今回は分布を変化させずにそのままzスコアを求めて行きます。それぞれのデータの平均と標準偏差、そしてzスコアによって得られた外れ値を表示します。今回はzスコアの有意水準を2に設定します。
#[IN]:
#ヒストグラムを作成するための関数を定義
def get_zscore(input_df):
#入力のコピーを作成
output_df=input_df.copy()
#詳細を表示するデータの列を指定
num_list=["sepal_length","sepal_width","petal_length","petal_width"]
#指定した列分繰り返す
for i in range(len(num_list)):
#列の平均を求める
mean=output_df[num_list[i]].mean()
#列の標準偏差を求める
std=output_df[num_list[i]].std(ddof=0)
#zスコアを求める
zscore=(output_df[num_list[i]]-mean)/std
#列名、平均、標準偏差、外れ値を表示
print(str(num_list[i]))
print("平均は:"+str(mean))
print("標準偏差は:"+str(std))
print("外れ値は↓")
print(str(output_df[num_list[i]][(zscore<-2)|(zscore>2)]))
print("*********************")
return output_df
関数が定義できたので、setosaについての外れ値検出を行います。今回は有意水準が2なので、データ全体の95.44%から外れた値を外れ値にしています。
#[IN]: #setosaのデータでのzスコアによる外れ値を表示 setosa_df=get_zscore(setosa_df)
#[OUT]: sepal_length 平均は:5.005999999999999 標準偏差は:0.348946987377739 外れ値は↓ 13 4.3 14 5.8 Name: sepal_length, dtype: float64 ********************* sepal_width 平均は:3.428000000000001 標準偏差は:0.3752545802518604 外れ値は↓ 15 4.4 33 4.2 41 2.3 Name: sepal_width, dtype: float64 ********************* petal_length 平均は:1.4620000000000002 標準偏差は:0.17191858538273286 外れ値は↓ 13 1.1 22 1.0 24 1.9 44 1.9 Name: petal_length, dtype: float64 ********************* petal_width 平均は:0.2459999999999999 標準偏差は:0.10432641084595984 外れ値は↓ 23 0.5 43 0.6 Name: petal_width, dtype: float64 *********************
setosaの外れ値はsepal_lengthに2個、sepal_widthに3個、petal_lengthに4個、petal_widthに2個検出されたことがわかりました。次はversicolorについての外れ値を検出して詳細を表示してみます。
#[IN]: #versicolorのデータでのzスコアによる外れ値を表示 versicolor_df=get_zscore(versicolor_df)
#[OUT]: sepal_length 平均は:5.936 標準偏差は:0.5109833656783752 外れ値は↓ 50 7.0 57 4.9 Name: sepal_length, dtype: float64 ********************* sepal_width 平均は:2.7700000000000005 標準偏差は:0.31064449134018135 外れ値は↓ 60 2.0 85 3.4 Name: sepal_width, dtype: float64 ********************* petal_length 平均は:4.26 標準偏差は:0.4651881339845204 外れ値は↓ 57 3.3 93 3.3 98 3.0 Name: petal_length, dtype: float64 ********************* petal_width 平均は:1.3259999999999998 標準偏差は:0.19576516544063702 外れ値は↓ 70 1.8 Name: petal_width, dtype: float64 *********************
versicolorの外れ値はsepal_lengthに2個、sepal_widthに2個、petal_lengthに3個、petal_widthに1個検出されたことがわかりました。次はvirginicaについての外れ値を検出して詳細を表示してみます。
#[IN]: #virginicaのデータでのzスコアによる外れ値を表示 virginica_df=get_zscore(virginica_df)
#[OUT]: sepal_length 平均は:6.587999999999998 標準偏差は:0.6294886813914925 外れ値は↓ 106 4.9 131 7.9 Name: sepal_length, dtype: float64 ********************* sepal_width 平均は:2.9739999999999998 標準偏差は:0.319255383666431 外れ値は↓ 117 3.8 119 2.2 131 3.8 Name: sepal_width, dtype: float64 ********************* petal_length 平均は:5.552 標準偏差は:0.5463478745268441 外れ値は↓ 117 6.7 118 6.9 122 6.7 Name: petal_length, dtype: float64 ********************* petal_width 平均は:2.026 標準偏差は:0.2718896835115301 外れ値は↓ 134 1.4 Name: petal_width, dtype: float64 *********************
virginicaの外れ値はsepal_lengthに2個、sepal_widthに3個、petal_lengthに3個、petal_widthに1個検出されたことがわかりました。
3種類とも外れ値の検出数が箱ひげ図の時よりも多いことが分かるかと思います。今回は有意水準が2でしたが、値によってはもう少し厳しくしたり、緩くしたりすることができます。外れ値の検出方法は様々ですが、最終的には自分の判断で有意水準を決める必要があります。そのため、それらを判断するためのドメイン知識というのが重要になってくるのです。
まとめ
今回は外れ値について解説と実装を行ってきました。本稿を読んでいただければご理解いただけるように、機械学習の勉強は外れ値一つとってもこれだけの量の知識が広がっています。数日勉強して身につくレベルではありませんが、だからこそ機械学習エンジニアが重宝されているとも言えます。今回の記事が本稿を読まれている方々の助けになれば幸いです。
codexaでは機械学習初学者に向けたコースを複数提供しています。
機械学習 準備編 無料講座
是非、皆様のご受講をお待ちしております。

