機械学習をやってみたいけど何から初めて良いか解らないと思ったことはありますか?もしそうでしたら、この記事はそんな方に向けて書かれています!
本記事では「TensorFlow 入門」として、Googleが提供する機械学習フレームワークである「TensorFlow」を使って、不動産価格を予測する流れをまとめました。概要は下記の通りです。
- プログラミング経験がある方が対象
- 環境構築不要!ブラウザのみで可能
- TensorFlowの基礎的な使い方が学べます
- 機械学習の基礎が学べます
- 所要時間の目安は1〜3時間程度
本記事では初心者対象として、数式を用いた厳密な説明は行なっておりません。より直感的に「機械学習」と「TensorFlow」を解説していきます。それでは、早速やってみましょう!
この記事の目次
TensorFlowとは?
TensorFlow(読み:テンソルフロー)とは、グーグルによって開発された高速数値解析用のPythonライブラリです。ディープラーニングやニューラルネットワークを構築するのに使われます。また、TensorFlowをバックエンドとしたラッパーライブラリも多く出回っています。
グーグルによって開発され、今でも定期的にアップデートが行われています。中身はC++で動いていますが、ユーザーが簡単に実装できるようにpythonのインターフェースが用意されています。
他のディープラーニング向けのライブラリと違い、TensorFlowは研究開発と生産システムへの導入の両方を目的として開発されました。グーグルで使われている人工知能RankBrainにもTensorFlowが使われています。
そもそもTensor(テンソル)とは?
テンソルとは多次元のデータを表すのに使われる高次元配列のことです。配列を扱うライブラリは他にもNumpyなどがありますが、TensorFlowではテンソルから直接関数を導き出したり自動的に微分を計算したりすることができます。本記事では厳密な解説は割愛しますが、テンソルは下記の図のように高次元の配列です。

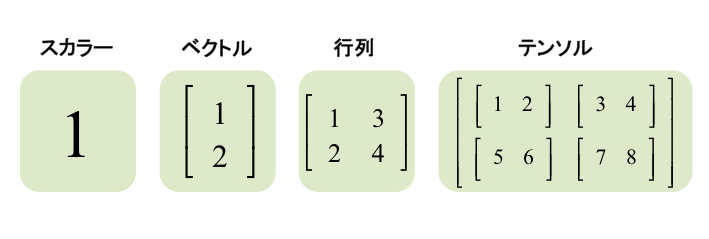
テンソルを深く理解するのには前提となる知識が必要ですが、機械学習では「ベクトル」や「行列」の理解は必須の知識です。(参照:機械学習に必要な基本の線形代数を学ぼう)
TensorFlowの仕組み(データフローグラフ)
TensorFlowは命令型プログラミングとは異なり、「データフローグラフ」と呼ばれるグラフを作り、グラフにデータを入力することで結果が出力されるという流れを理解する必要があります。
言葉で聞くと難しいので、データフローグラフを簡略化した図式を用いて紐解きましょう。まずは下の図を見てください。
こちらで、赤のボックスは「入力値」を表しており、青のボックスは「ノード」、矢印は「エッジ」を表しています。始まりは一番左の入力「3」と「5」から始まり、次の「ノード」では加算の処理を行っています。加算された値「8」と新しい入力値「9」が次のノードで乗算の処理を行い、最終的に56の値を出力しています。
この図式のように、TensorFlowではノード(処理を加える)やエッジ(加えた処理を次へ送る)などを事前に設計して、実行を行い処理を行う流れが一般的です。
言葉だけで見ると解りづらいですが、後ほどPythonを使ってコーディングしますので、より明確に理解できるかと思います。
なぜTensorFlowが使われるのか?
機械学習には多種多様の手法やアルゴリズムが存在します。TensorFlowを使うことで、機械学習のアルゴリズムや手法を効率的かつ簡単に実装をすることが可能です。
TensorFlowには機械学習で必要な演算処理や関数などが多数用意されています。
例えば線形回帰やディープラーニングでも一般的に使われる最適化アルゴリズムに「最急降下法」があります。本来であればアルゴリズムの処理をスクラッチでコーディングしなくてはいけません。しかし、TensorFlowを使うことで、容易に最急降下法の処理を組み込むことが可能になります。
機械学習のプロセスを効率化してくれるライブラリはTensorFlowだけではありません。TensorFLowと並んで、世界的に人気のある「Scikit-learn(サイキット・ラーン)」も耳にした事がある方も多いかと思います。
Scikit-learnにはランダムフォレストやサポートベクターマシンなど、機械学習の手法がそのまま使える形で用意されています。対してTensorFlowは、NumpyやPandasに感覚は近く、手法を実装するために利用をするものです。
TensorFlowの特徴をいくつか紹介したいと思います。
携帯性 ・スケーラビリティ
TensorFlowはデスクトップ、サーバー、モバイルなどあらゆるプラットフォーム上で同一のコードで実行することができます。CPUからGPUへの切り替えもコードの書き換え無しでできます。完成した学習モデルのモバイルへの移植にも優れています。
TensorBoard
TensorFlow内のあらゆるデータを可視化するときに便利なのがTensorBoardです。TensorBoardはTensorFlowをインストールするときに一緒に付属する可視化ツールです。TensorFlowで構築したデータフロー図を図面化することができます。他にもコスト関数や評価指標をプロットしたり、学習過程でのテンソルの変化をヒストグラムにしたり、実行時間やメモリ使用量などの学習に関するメタデータを集計したり、画像を表示するなどができます。
コミュニティ
TensorFlowはコミュニティが大きく、サポート体制が充実しています。なにかわからないことがあれば公式ページで世界中の人に質問したり、同じようなトラブルを抱えた人の質問への回答を見ることができます。また、グーグルによって管理されているので、今後もアップデートを通して性能が向上していくことが期待できます。
それでは、次のセクションからはPythonとTensorFlowを実際に使ってみましょう!
STEP1 実行環境について
本記事ではブラウザのみで機械学習に必要なライブラリ環境の利用が可能な「Google Colab(読み:グーグル・コラボ)」を利用します。利用にはGoogleの無料会員登録が必要です。まずは、下記のURLでGoogle Colabへアクセスをお願いします。
> Python3でGoogle Colabの新しいノートブックを作成
Googleのアカウントへログインされていない方は、下記のようにログインを促すポップアップが出ます。手順に沿ってログインをしましょう。
ログインが完了すると、下の図のような画面へ遷移します。これはJupyter Notebook(読み:ジュピター・ノートブック)と呼ばれており、Pythonのプログラムの実行や説明文章などを管理できるデータ分析の世界で頻繁に使われるツールです。(参照:Jupyter Labとは?)
Jupyter Notebookは「.ipynb」のファイル形式となります。解りやすいように、新規で立ち上げたノートブックの名前を変更してあげましょう。上の図の赤枠をクリックすることで名前の編集が可能です。名前はなんでも大丈夫です。(私はTensorFlow_Codexa.ipynbと名付けました)
それでは試しに本記事で使うPythonライブラリをインポートしてみましょう。上記の図の通り最初のコードセル(入力欄)へ下記のコードを入力してShift + Enterでコードを実行しましょう。
# テンソルフロー import tensorflow as tf # 計算やデータ処理のライブラリ import numpy as np import pandas as pd # データ可視化のライブラリ import matplotlib.pyplot as plt # データセットの取得&処理のライブラリ from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split # インポートの確認 print(tf.__version__) print(np.__version__) print(pd.__version__)
コードを実行すると下の図のように、数値が出力されているのが確認できるかと思います。Jupyter Notebookでは、セル上でPythonのコードを実行&管理ができるため、多くの機械学習エンジニアが標準的に利用しています。
本記事ではTensorFlowを含めて5つの基本的なPythonライブラリを使用します。計算処理を効率的に行う「Numpy(読み:ナンパイ)」や、大規模データを扱いやすくする「Pandas(読み:パンダス)」も使用します。これらのライブラリは機械学習では必須のツールですので、より詳しい操作方法は下記の無料コースをご覧ください。
・Numpy 入門コース(無料)
・Pandas 入門コース(無料)
STEP2 データセットと問題定義
本記事で扱うデータセットを紐解きましょう。今回はScikit-learnに組み込まれている「Boston house-prices(ボストン市の住宅価格)」のデータセットを利用します。概要は下記の通りです。
こちらのデータセットはボストン市内のエリアに属する情報データと、そのエリアの不動産価格の中央値が与えられたデータです。
| 概要 | |
|---|---|
| データセット名前 | boston house-prices dataset |
| データ発行元 | カルフォルニア大学アーバイン校 |
| データ数 | 506レコード |
| 特徴量 | |
| CRIM | 1人あたりの犯罪発生率 |
| ZN | 2.5万平方フィート以上の居住エリアの割合 |
| INDUS | 小売業以外のビジネスの土地の割合 |
| CHAS | チャールズ川の周辺かどうか(1=周辺、0=それ以外) |
| NOX | 一酸化窒素の濃度 |
| RM | 住居の部屋の平均数 |
| AGE | 1940年より前に建築された物件の割合 |
| DIS | 5つの雇用センターへの距離(重み付け済み) |
| RAD | 環状道路へのアクセスの容易度 |
| TAX | 1万ドルあたりの固定資産税総額 |
| PTRATIO | 教師と児童の比率 |
| B | 黒人の比率 |
| LSTAT | 低所得層の人口の割合(%) |
| ターゲット | |
| MEDV | 当該地域に属する不動産価格の中央値(単位:1千ドル) |
上記で「特徴量」と「ターゲット」とありますが、機械学習で使われる初歩的な用語です。特徴量とは今回のケースでいうエリアごとのデータ(例:犯罪発生率や環状道路へのアクセスなど)を指します。
対してターゲットとは機械学習を使って推測したい値であり、今回のケースでは「エリアの不動産価格の中央値」です。
今回の例題では、「特徴量」と「ターゲット」を機械学習アルゴリズムにより学習を行い、新しい未知のデータの特徴量を使ってそのエリアの不動産価格を予測するのが目的となります。
それでは、このボストンの不動産データをScikit-learnから読み込んでみましょう。下記のコードでは、データセットを読み込み、さらに取り扱いやすいようPandasのデータフレーム形式への変換を行います。各自、Google Colabの2番目のコードセルに入力してShift + Enterでコードを実行してみてください。
# データの読み込み boston = load_boston() # Pandasのデータフレーム形式へ変換 df = pd.DataFrame(boston.data, columns=boston.feature_names) df['target'] = boston.target # データの最初の5行を表示 df.head()
-- 出力 CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT target 0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0 1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6 2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7 3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94 33.4 4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33 36.2
ご覧の通りデータの最初五行が出力されています。前述しましたが、1行毎にボストン市内のエリアの情報と、そのエリア内の不動産価格の中央値(1千ドル単位)が格納されています。
下記は上のデータの1行目と4行目の一部を抜粋してまとめたテーブルです。データを紐解く目的のため、解りやすいデータを抜粋しました。
ご覧の通り1行目と4行目のエリアを比べると、不動産価格に約1万ドル(約1 10万円)の差が出ています。それぞれの地域の特徴量の一部を見てみると、1行目のエリアでは犯罪発生率が非常に高く、また低所得層の人口の割合も高いです。
このように特徴量とターゲットには関係性があります。本記事では、機械学習で最も初歩的かつシンプルな「線形回帰」という手法を用いてターゲットの推測を行います。
今回は線形回帰の詳細については渇愛をしますが、機械学習をこれから勉強しようと考えている方は、ぜひ下記の線形回帰入門コースの受講をご検討ください。
STEP3 データの前処理
データの読み込みが完了しましたので、次は機械学習アルゴリズムが学習を効率的に行えるよう「データの前処理」を行いましょう。まずは特徴量とターゲットを切り分けます。
# 特徴量とターゲットに切り分け X_data = np.array(boston.data) y_data = np.array(boston.target) # 1行目のデータの特徴量(X)とターゲット(y)を確認 print(X_data[0:1]) print(y_data[0:1])
-- 出力 [[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01 4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00]] [24.]
次に特徴量の正規化を行いましょう。正規化(読:せいきか)とはそれぞれの特徴量のレンジを整える処理のことです。英語ではNormalization(ノーマライゼーション)やFeature Scaling(フューチャー・スケーリング)と呼ばれています。
例として「1人あたりの犯罪発生率(CRIM)」と「教師と児童の比率(PTRATIO)」を考えてみましょう。1行目のエリアのCRIMの値は0.00632とあり、対してPTRATIOの値は15.3です。それぞれの特徴量の値に大きな乖離が存在します。
機械学習のアルゴリズム/手法の中には、このように特徴量のデータのレンジが大きく異なると、モデルを訓練する際に不具合を起こしてしまう場合があります。どのような影響があるかはアルゴリズム/手法により異なります。
正規化の手法はいくつか存在します。今回はシンプルに各特徴量の平均を0、分散を1とする処理を行いましょう。計算方法として、各特徴量の平均値を求め、それぞれの特徴量の値から平均値を引いたものを標準偏差で割ります。標準偏差はデータの散らばり具合を示す統計の指標です。詳しくは、無料の統計入門コースをご参照ください。
# 正規化
def norm(data):
mean = np.mean(data, axis=0)
std = np.std(data, axis=0)
return (data - mean) / std
# データを変更
X_data = norm(X_data)
print(X_data[0:1])
-- 出力 [[-0.41771335 0.28482986 -1.2879095 -0.27259857 -0.14421743 0.41367189 -0.12001342 0.1402136 -0.98284286 -0.66660821 -1.45900038 0.44105193 -1.0755623 ]]
上の出力は正規化した後の1行目の特徴量の値です。1行目のCRIMの元の値は0.00632でしたが、正規化の処理を行なった後は-0.41771335となっているのが確認できます。
正規化の処理を行う必要があるアルゴリズムと必要でないアルゴリズムがあります。今回の線形回帰では、最適化アルゴリズムである「最急降下法」を用いますので、正規化を行うことで、より効率よく最適化を行うことが可能になります。
次の前処理の作業として、特徴量のデータの最初の列に数字の「1」を追加してあげましょう。これは、データを機械学習アルゴリズムへ学習させる際に、計算をスムーズにしてくれる意味があります。(詳しくは実践 線形回帰をご参照ください)
# 1を追加する前のサイズ print(X_data.shape) # 1を作成 ones = np.ones((506, 1)) # 1を追加 X_data = np.c_[ones, X_data] X_data.shape
-- 出力 (506, 13) (506, 14)
ご覧の通り元々13個あった特徴量に全て値が「1」の列が追加され、506行14列のデータとなりました。前処理の最後の工程として、訓練データとテストデータへ切り分けてあげましょう。
機械学習では一般的にデータセットを「訓練(Training)」と「テスト(Test)」へ分割を行ないます。理由としては訓練データで機械学習モデルへ学習を行い、学習させていないテストデータを使ってモデルの予測精度を評価する目的があります。
一般的に訓練データ8割/テストデータ2割(で分割を行います。Scikit-learnには訓練/テストデータの分割を瞬時に処理をしてくれる関数(train_test_split)が用意されていますので、そちらを利用しましょう。
# 訓練データとテストデータへ切り分け X_train, X_test, y_train, y_test = train_test_split(X_data, y_data, test_size=0.2, random_state=42) y_train = y_train.reshape(404,1) y_test = y_test.reshape(102,1) print(X_train.shape) print(y_train.shape) print(X_test.shape) print(y_test.shape)
-- 出力 (404, 14) (404, 1) (102, 14) (102, 1)
元データでは506レコードありましたが、その8割にあたる404が訓練データへ、残りの102がテストデータへ分割されています。最低限ではありますが、データの前処理がこれで完了しました。
STEP4 線形回帰モデルの訓練
ではいよいよ本題である「TensorFlow」を使って、線形回帰モデルへ訓練データを学習させてみましょう。まずはTensorFlowで線形回帰モデルの設定を行います。
# 学習率とエポック(反復処理回数) learning_rate = 0.01 training_epochs = 100 # 特徴量の数 n_dim = X_data.shape[1] # 特徴量(X)とターゲット(y)のプレースホルダー X = tf.placeholder(tf.float32,[None,n_dim]) Y = tf.placeholder(tf.float32,[None,1]) # 係数(W)と定数項(b)の変数 W = tf.Variable(tf.ones([n_dim,1])) b = tf.Variable(0.0)
線形回帰モデルの構築を行うために必要な設定を行いました。次にコスト関数と最適化の処理を作ります。
# 線形モデル y = tf.add(b, tf.matmul(X, W)) # コスト関数 cost = tf.reduce_mean(tf.square(y - Y)) # 最適化 training_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
コスト関数とは、「実際の値とモデルが推測した値の誤差を指標化」したものです。この「誤差」をなるべく最小限にすることで、線形回帰のモデルはより近しい予測をすることが可能になる訳です。
下の図はこの流れを簡略化したものです。ご覧の通り最初の誤差(cost)は「10」とありますが、反復処理で計算を繰り返すたびに誤算が小さくなっていくのが確認できます。
上のコードの一番最後の「training_step」に注目すると分かりますが、誤差(cost)を最小化する処理が加えられているのが分かります。
では、いよいよ訓練データ(X_trainとy_train)を使ってモデルの訓練を行いましょう。変数の初期化を行い、セッションを開始させます。
# 初期化
init = tf.global_variables_initializer()
# モデル訓練開始
sess = tf.Session()
sess.run(init)
for epoch in range(training_epochs):
sess.run(training_step, feed_dict={X:X_train, Y:y_train})
cost_history = np.append(cost_history, sess.run(cost, feed_dict={X:X_train, Y:y_train}))
if epoch % 100 == 0:
W_val = sess.run(W)
b_val = sess.run(b)
これで訓練データの特徴量とターゲットの学習が完了しました。上記コードを見ると分かりますが、cost_historyとして反復処理毎に誤差(cost)の履歴を取得しています。
2回目、50回目、100回目のコストを確認してみましょう。正しく処理が行われていれば、誤差(cost)は減少しているはずです。
# 誤差(cost)を確認 print(cost_history[1]) print(cost_history[50]) print(cost_history[100])
-- 出力 559.8623657226562 35.80818557739258 25.0402889251709
ご覧の通り最初は559とあったコストですが、最適化アルゴリズムでコストの最小化の処理を行うことで、反復計算毎に減少しているのが確認できます。
STEP5 テストデータで予測
では、訓練済みのモデルを使ってテストデータから不動産価格の予測を行なってみましょう。上記のコードを注視すると分かりますが、モデルには訓練データ(X_trainとy_train)のみを使っており、テストデータは一切使っていません。
では、予測をしてみましょう。
# テストデータを使って予測
pred_test = sess.run(y, feed_dict={X: X_test})
これで予測が完了です。では、実際にどれほどの精度で予測できているのか確認してみます。実際の不動産価格(y_test)と予測した不動産価格(pred_test)の対比表を作ってみます。
pred = pd.DataFrame({"実際の不動産価格":y_test[:,0], "予測した不動産価格":pred_test[:,0]})
pred.head()
-- 出力 予測した不動産価格 実際の不動産価格 0 26.497128 23.6 1 33.817684 32.4 2 16.889990 13.6 3 22.577736 22.8 4 18.896347 16.1
ご覧の通り、それなりの予測ができていますね!例えば一番上の行を確認してみると、このエリアの実際の不動産価格は約26.4千ドルですが、エリアの情報(特徴量)を使って予測をしたところ23.6千ドルと予測することが出来ています。
まとめ
本記事ではTensorFlowの基礎的な使い方として、実際のデータセットを用いてシンプルな機械学習手法(線形回帰)を用いて予測を行なってみました。
実際にコードを動かしてみて如何でしたでしょうか?本記事にも使われていますが、機械学習をしっかり理解するには「線形代数」や「統計」の基礎、さらにNumpyやPandasなどPythonの基礎ライブラリを使いこなす必要があります。
codexaでは機械学習準備編として、無料でコースを公開しています。是非、これらのコースの受講をご検討ください。
・Numpy 入門(無料)
・Pandas 入門(無料)
・Matplotlib 入門(無料)
・線形代数(無料)
・統計基礎(無料)
また、すでに機械学習の基礎知識がある方に向けて、機械学習の様々な手法を詳しく解説したチュートリアルも公開しています。
・実践 線形回帰
・実践 ロジスティック回帰
・決定木とランダムフォレスト
・サポートベクターマシン
・ナイーブベイズ(単純ベイズ分類器)
以上となります!最後まで記事をご覧頂き、ありがとうございました。

